=> – импликация – логическое следствие; означает «если, то …».
ТОЧКА
Метод проекций
В основе правил построения изображений лежит метод проекций. Суть метода заключается в том, что каждой точке трехмерного пространства соответствует определенная точка двухмерного пространства плоскости. Изучение его начинают с построений проекций точки, т. к. любой геометрический объект может рассматриваться как множество точек, заданных по определенному закону.
Этот геометрический объект отображается на плоскость по закону проецирования. Процесс отображения называется проецированием. Результатом такого отображения является изображение объекта, которое называется проекцией.
Для построения проекции геометрического объекта задают аппарат проецирования, в который входит объект проецирования,например, точка А,и плоскость проецирования Р (иногда ее называют картинной плоскостью), не проходящая через точку А (рис. 1).Для получения изображения точки А на плоскость Р через нее проводят проецирующий луч до его пересечения с плоскостью Р в точке а. Полученную точку а называют проекцией точки А. Проекция (лат. projectio – выбрасывание вперед).
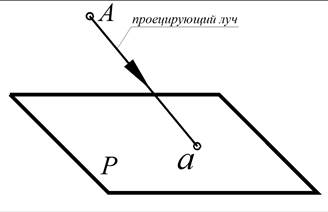
Рис. 1. Проецирование точки А
Виды проецирования
- Центральное проецирование
Задан аппарат проецирования: центр проекций S, плоскость проецирования Р.
В результате центрального проецирования на плоскости Р получится центральная проекция любого геометрического объекта. На рис. 2 показано построение центральной проекции отрезка АВ. Проекционный метод изображения предметов основан на их зрительном представлении.
Если соединить все точки предмета прямыми линиями (проекционными лучами) с постоянной точкой S (центр проекции), в которой предполагается глаз наблюдателя, то на пересечении этих лучей с какой-либо плоскостью получается проекция всех точек предмета. Таким образом получаем на плоскости перспективное изображение предмета или центральную проекцию.
Свойства центральных проекций:
– проекция точки – точка;
– проекция прямой – прямая;
– если точка принадлежит прямой, то проекция этой точки принадлежит проекции прямой.
2. Параллельное проецирование – частный случай центрального проецирования, когда центр проецирования бесконечно удален. Поэтому в аппарат проецирования входит: направление проецирования S и плоскость проецирования Р. При этом проецирующие лучи рассматривают как прямые, параллельные между собой и параллельные заданному направлению проецирования S (рис. 3).

Рис. 2. Центральное проецирование отрезка АВ
Рис. 3. Параллельное проецирование:
а – косоугольное отрезка АВ; б – ортогональное точки А
В зависимости от направления проецирования параллельные проекции могу быть:
– ортогональными (прямоугольными) проекциями – проекционные лучи падают перпендикулярно к картинной плоскости Р (рис. 3б);
– косоугольная проекция – проекционные лучи падают не перпендикулярно к картинной плоскости Р (рис. 3а).
Свойства параллельных проекций:
– проекция точки – точка;
– проекция прямой – прямая;
– если точка принадлежит прямой, то проекция этой точки принадлежит проекции этой же прямой;
– проекции параллельных прямых параллельны;
– отношение отрезков прямой равно отношению их проекций.
Ортогональное проецирование имеет ряд преимуществ перед центральным и косоугольным параллельным проецированием:
– простота построений изображения геометрического объекта;
– точность – сохранение точных форм и размеров проецируемой фигуры на чертеже;
– наглядность –чертеж должен создавать пространственное представление о форме геометрического объекта;
– обратимость – возможностьвосстановления оригинала по проекционным изображениям геометрического объекта.
Источник: infopedia.su
Что значит знак : в геометрии?
Денежный знак училке по геометрии означает пятёрку без опроса у доски или за контрольную. (В геометрии — соотношение, подобие, пропорциональность величин).
Светлана Светова
Анна Николаева
Делимость или деление, точно не помню
Двоеточие является одним из возможных обозначений операции деления (при этом симметрично отбивается с обеих сторон) ; в другом значении отделяет знак отображения и его область определения и множество значений: запись «f: A→B» означает, что функция f отображает A на B (при этом пробел ставится только после двоеточия) .
Плюс: +
Минус: −
Знаки умножения: ×, ∙ (в программировании также
Знаки деления: :,
Источник: sprashivalka.com
Знак подобия в геометрии — правило и примеры обозначения
В учебниках по геометрии часто встречаются задачи на подобие фигур. Какой знак используется для обозначения подобия фигур? Какие фигуры называются подобными? Поговорим обо всем этом в нашей статье.
Определение и знак подобия в геометрии
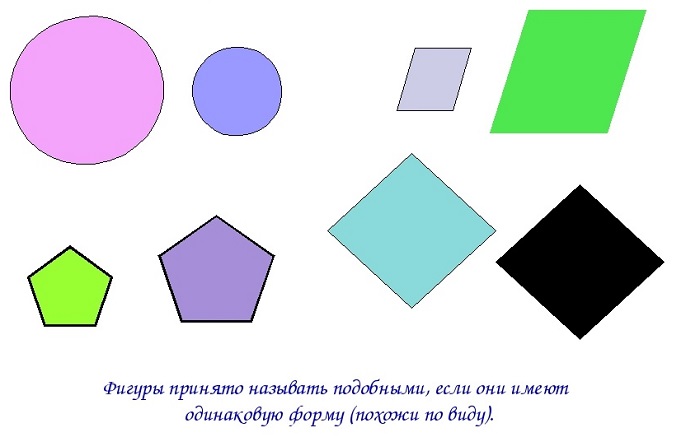
Подобными называются фигуры, если одна из них представляет уменьшенную копию другой.
На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.

Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:
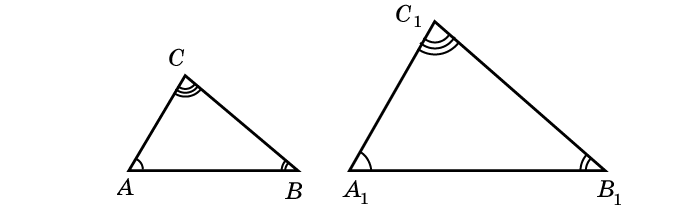
∆ABC ~ ∆A 1 B 1 C 1 — треугольники ABC и A1B1C1 подобны. Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо: 1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.
Коэффициент подобия треугольников и знак подобия
Часто сверху знака подобия выставляют коэффициент подобия треугольников:
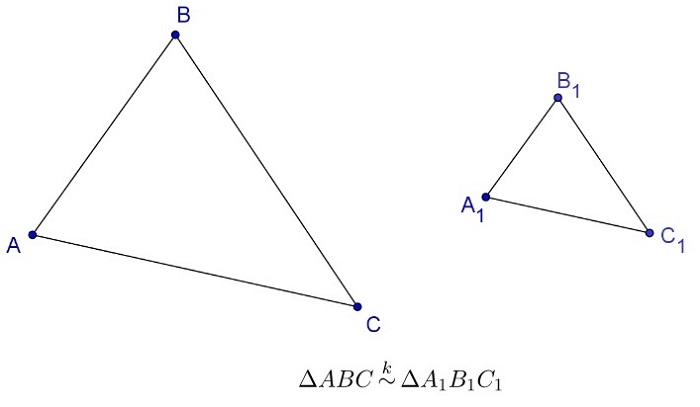
В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности. В алгебре высказываний знаком ~ обозначают логическую операцию «эквиваленция». При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):
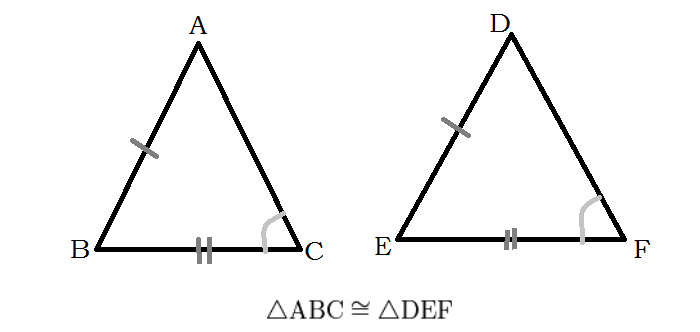
Признаки подобия прямоугольных треугольников
Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными. Два катета: общая пропорциональность катетам одного прямоугольного треугольника к катетам второго делает их подобными. Катет и гипотенуза: пропорциональность катета и гипотенузы одного прямоугольного треугольника к катету и гипотенузе второго прямоугольного треугольника делает их подобными.
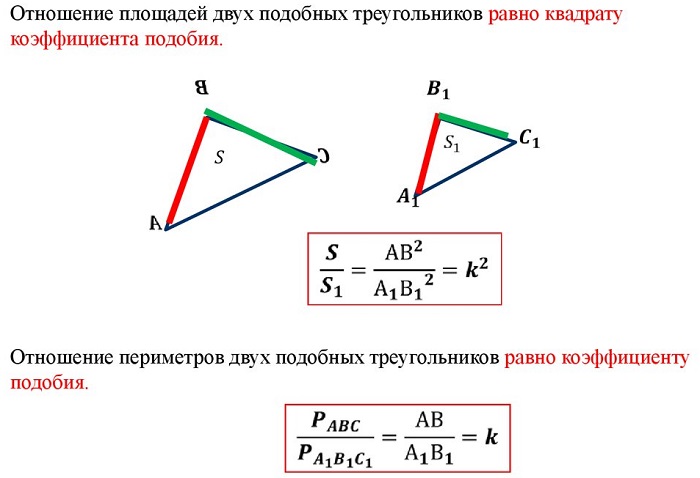
- треугольник ∆ABC и треугольник ∆A1B1C1 считаются подобными при равнозначности углов и пропорциональности сторон;
- отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство подобия треугольников через среднюю линию
Имеется треугольник ∆ABC, mn — средняя линия. M лежит на AB, N лежит на BC.
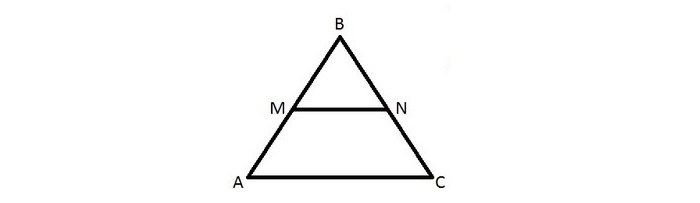
Требуется доказательство подобия треугольников ∆MBN и ∆ABC.
Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:
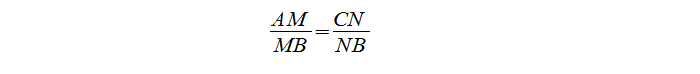
Отсюда делаем вывод, что ∆MBN ~ ∆ABC по II признаку подобия треугольников, что и требовалось доказать.
Примеры решения задач по геометрии на тему «Подобие треугольников»


Источник: nauka.club
