Обычно у детей младшего школьного возраста неплохо развита механическая память, которая так необходима для выучивания правил. Но многие, особенно творческие личности, не выносят зубрежки. Кажется, что они отстают в школьной программе, – а на самом деле к ним нужен особый подход. Если Вы задаетесь вопросом, как помочь ребенку с изучением таблицы умножения.
На механической памяти, по сути, строится все начальное образование. Но она может быть скомпенсирована любознательностью, острым умом и творческими способностями ребенка. Мои советы помогут Вам узнать, как быстро выучить таблицу умножения с применением нестандартного подхода. Это проще простого – убедитесь сами!
Упрощаем таблицу
1. Что больше всего смущает ребенка (да и Вас, откровенно говоря), когда Вы смотрите на стройные ряды цифр в таблице умножения? Огромное количество правил – нетрудно сосчитать, что их ровно сто: десять столбцов и десять строк.
Как же ребенку выучить таблицу?
Для начала убедимся в том, что правил, на самом деле, гораздо меньше. Ни одному ребенку не составит труда выучить первый столбец – любое число, умноженное на единицу, равно самому себе. И с последним проблем ровно столько же – умножили на десять, значит, просто дописали справа от числа ноль.
Слагаемые. Сумма. Уменьшаемое. Вычитаемое. Разность | Математика 1 класс #14 | Инфоурок
Сто правил минус двадцать (два столбца) – уже 80.
2. Выучивая таблицу с ребенком, легко показать ему, что от перестановки сомножителей произведение не меняется. В первом классе он уже имел дело с переменой мест слагаемых, где царит тот же закон. То есть если 6 х 3 = 18, то и 3 х 6 = 18. Сколько правил можно сразу отбросить после выяснения этой несложной истины? Еще 44, посчитайте сами.
А 80 минус 44 – это уже 36!
3. Продолжаем делать таблицу как можно проще. Ваш ребенок хорошо умеет складывать два числа и знает, что 5 + 5 = 10, 6 + 6 = 12. Пришла пора объяснить ему связь между умножением и сложением: число, умноженное на два, — это число, сложенное с самим собой.
То же касается и других столбцов таблицы (на три – три раза сложенное и т.д.), но это уже сложнее, а с умножением на два проблем в сознании ребенка возникать не должно. Сколько правил уйдет из второго столбца? После предыдущих шагов их там осталось 8, а 36 минус 8 равно 28.
4. Далее разделаемся с другими запоминающимися правилами – умножение числа на самого себя(2 х 2, 6 х 6), умножение числа на 5 (тоже характерно, окончание всегда либо 5, либо 0: 6 х 5 = 30, 7 х 5 = 35). У Вас уже не должно остаться вопросов, как выучить таблицу умножения из 15 строк.
5. Обязательно повторите с ребенком выученные правила, сгруппированные по столбцам. Ему уже не составит никакого труда доучить то, чего он в этом столбце еще не знает.
6. Наконец, для закрепления материала пройдитесь по правилам вразнобой, выхватывая их из таблицы наугад. Вы удивитесь – но Ваш ребенок уже будет знать все! Если тратить по дню на каждый из шагов нашей инструкции, выходит, что выучить таблицу умножения без всякой головной боли можно меньше, чем за неделю!
Уменьшаемое вычитаемое разность. Математика 1 класс
7. Так же на основе умножения ребенок должен знать и таблицу деления.
Например 32:8 = ( Ребенок вспоминает что 32 это 8х4 значит 32:8 будет 4.
РЕБЕНОК ДОЛЖЕН УМЕТЬ ОТВЕЧАТЬ НА ВОПРОСЫ:
ПРИ УМНОЖЕНИИ КАКИХ ЧИСЕЛ МОЖНО ПОЛУЧИТЬ ЧИСЛО 36? 25?16? И Т.Д.
Вы убедились в том, что можно легко выучить таблицу умножения? В заключение – еще несколько полезных советов на закрепление
- Можно порекомендовать детям самостоятельно нарисовать таблицу яркими красками (зрительная память), придумать аналогии и целые истории по каждому правилу (ассоциативная и образная память). Можно использовать игры с карточками, предметами быта и даже едой типа чипсов. Для запоминания «сложных» правил существуют методы, которые могут оказаться более эффективными, чем заучивание, например, «умножение на пальцах». В любом случае следует выбирать самый быстрый способ, то есть – более всего понятный ребенку.
ЗАПОМНИТЕ: ТАБЛИЦУ УМНОЖЕНИЯ И ДЕЛЕНИЯ ПОВТОРЯТЬЕЖЕДНЕВНОИ НЕ ПО ПОРЯДКУ.
Правила по математике для заучивания летом !
первое слагаемое + второе слагаемое = сумма
уменьшаемое — вычитаемое = разность
первый множитель * второй множитель = произведение
делимое : делитель = частное
1. Чтобы найти НЕИЗВЕСТНОЕ СЛАГАЕМОЕ необходимо из СУММЫ вычесть ИЗВЕСТНОЕ СЛАГАЕМОЕ
2. Чтобы найти УМЕНЬШАЕМОЕ, нужно к РАЗНОСТИ прибавить ВЫЧИТАЕМОЕ.
Чтобы найти ВЫЧИТАЕМОЕ, нужно из УМЕНЬШАЕМОГО вычесть РАЗНОСТЬ.
3. Чтобы найти НЕИЗВЕСТНЫЙ МНОЖИТЕЛЬ необходимо ПРОИЗВЕДЕНИЕ разделить на ИЗВЕСТНЫЙ МНОЖИТЕЛЬ.
4. Чтобы найти ДЕЛИМОЕ, нужно ЧАСТНОЕ умножить на ДЕЛИТЕЛЬ.
Дата добавления: 2018-08-06 ; просмотров: 1098 ; Мы поможем в написании вашей работы!
Поделиться с друзьями:
Источник: studopedia.net
Вычитание
Вычитание есть такое действие, в котором отнимают меньшее число от большего. При вычитании целых чисел большее число уменьшается на столько единиц, сколько их содержится в меньшем. Вычесть одно число из другого значит убавить одно число другим, поэтому вычитание есть действие обратное сложению.
В вычитании два данных числа называются уменьшаемым и вычитаемым , а искомое — разностью .
Уменьшаемым называют большее число, от которого отнимают другое. Оно уменьшается от вычитания.
Вычитаемым называют меньшее число, которое отнимают от большего.
Разностью называют вывод, полученный от вычитания. Разность определяет, чем одно число больше другого или показывает разницу между двумя числами.
Знак вычитания. Действие вычитания обозначается знаком — (минус).
Вычитание однозначных чисел
Чтобы обозначить, что из 9 нужно вычесть 6, пишут эти числа рядом, отделяя их знаком — (минус):
Разность между этими числами будет 3, и ход вычисления выражают словесно:
девять без шести равно трем.
Большее число 9 будет уменьшаемым, меньшее 6 вычитаемым, число 3 остатком.
Способы вычитания
Можно двумя способами вычесть одно число из другого:
- или можно отнять от большего числа столько единиц, сколько их содержится в меньшем. Так, из 9 вычесть 6 значит от 9 отнять 6. Число 3 будет искомый остаток;
- или можно к меньшему числу прибавлять по единице до тех пор, пока не получим большее число. Так, вычитая 6 из 9, мы к 6 прибавляем 3 единицы. Число единиц, которое нужно прибавить к меньшему числу, чтобы уравнять его с большим, определяет разность. Меньшее число с разностью должно равняться большему числу, следовательно, меньшее число и разность суть слагаемые, а большее — их сумма. На этом основано другое определение вычитания:
Вычитание есть такое действие, в котором по данной сумме и одному слагаемому отыскивается другое слагаемое.
В этом случае данная сумма есть уменьшаемое, данное слагаемое — вычитаемое, а искомая разность — другое слагаемое.
Вычитание многозначных чисел
Вычитание многозначных чисел основывается на том свойстве чисел, по которому вычесть число все-равно, что вычесть все его части. Из этого свойства видно, что вычесть какое-нибудь число все-равно, что вычесть последовательно все его единицы, десятки, сотни и т. д. Чтобы обозначить, что из числа 7228 нужно вычесть 3517, пишут:
и вычитают отдельно единицы из единиц, десятки из десятков и т. д.
Чтобы облегчить вычитание, подписывают меньшее число под большим так, чтобы единицы одинаковых порядков находились в одном вертикальном столбце, проводят черту, слева ставят знак вычитания — и под чертою подписывают разность.
Ход вычисления выражают словесно:
- Начинаем вычитание с простых единиц: 8 без 7 составляют 1; подписывают под единицами 1.
- Вычитаем десятки: 2 без 1 дают 1, подписываем под десятками 1.
- Вычитаем сотни. Пять нельзя вычесть из 2, поэтому занимаем у следующего высшего порядка (тысяч) единицу, что и обозначаем тем, что над 7 ставим точку. Единица каждого порядка содержит 10 единиц следующего меньшего порядка. Присоединяя эти 10 единиц к 2, получим 12; 12 без 5 составляют 7, подписываем под сотнями 7. Когда занимают единицу у высшего порядка, обозначают это тем, что ставят точку над порядком, у которого занимают.
- Вычитаем тысячи. Тысяч осталось вместо 7 только 6, ибо одна была взята. 6 без 3 составляют 3; подписываем под тысячами 3.
Ход вычисления выражают письменно:

Пример. Из 17004 вычесть 6025.
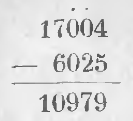
Из 4 нельзя вычесть 5. Занимаем единицу у десятков, следующего высшего порядка, но в этом порядке единиц нет; занимаем у сотен, — и сотен нет; занимаем у тысяч и обозначаем это точкой над цифрой 7.
Единица четвертого имеет 10 единиц третьего порядка. Взяв из них одну для десятков, оставляем их в сотнях только 9. Присоединив 10 к 4, имеем 14.
Производя вычитание, получим:
- для единиц 14 — 5 = 9
- для десятков 9 — 2 = 7
- для сотен 9 — 0 = 9
- для тысяч 6 — 6 = 0
Для десятков тысяч имеем 1, ибо эту цифру уменьшаемого переносим в разность без изменения.
Ход вычисления выразится письменно:
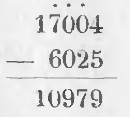
Из предыдущих примеров выводим правила вычитания:
- Чтобы сделать вычитание целых чисел, нужно вычитаемое подписать под уменьшаемым так, чтобы единицы одинаковых порядков стояли в одном вертикальном столбце, провести черту, под которою и подписать разность.
- Вычитание нужно начинать с простых единиц, то есть с первого столбца, и затем, переходя к следующим столбцам от правой руки к левой, вычитают десятки из десятков, сотни из сотен и т. д.
- Если цифра вычитаемого меньше цифры уменьшаемого, разность подписывают в том же столбце; если цифры равны, разность будет нуль. Если же цифра вычитаемого больше соответствующей цифры уменьшаемого, занимают единицу у следующего порядка уменьшаемого, отмечая это точкой, поставленной над цифрой, у которой занимают, прикладывают 10 к цифре уменьшаемого и производят вычитание. Цифру же с точкой считают на единицу меньше.
- Если при вычитании цифра уменьшаемого, у которого занимают, будет 0, за которым в уменьшаемом следуют тоже нули, то занимают у первой значащей цифры, ставя над нею и всеми промежуточными нулями точки. Цифру с точкой считают на единицу меньше, а нули с точкой считают за 9.
- Вычитание продолжают до тех пор, пока не получат полной разности.
- Лишние цифры уменьшаемого переносят в разность.

Зависимость между данными и искомыми вычитания
Из примера 9 — 6 = 3 видно, что
- Уменьшаемое равно вычитаемому, сложенному с разностью: 9 = 6 + 3.
- Вычитаемое равно уменьшаемому без разности: 6 = 9 — 3.
- Разность равна уменьшаемому без вычитаемого: 3 = 9 — 6.
Арифметическое дополнение. Разность между числом и ближайшей большей единицей называется арифметическим дополнением. Так, арифметическими дополнениями чисел 7, 79, 983 будут числа:
10 — 7 = 3
100 — 79 = 21
1000 — 983 = 17
Арифметическим дополнением иногда пользуются для облегчения арифметических вычислений.
Источник: maths-public.ru
