На этом форуме большое количество бывших олимпиадников, «тренеры» думаю тоже есть, но тем, связанных с подготовкой к олимпиадам я не нашел, хотя все внимательно просмотрел.
Думаю это было бы актуально очень многим, т.к. по моему мнению, выигрывают олимпиады не «гении», а те у кого была лучшая подготовка.
Во-первых, я вижу принципиальные различия между международными и всероссийскими. В международных, для успешного решения почти всех задач, достаточно быть эрудитом. Лично моя подготовка позволяла (в свое время) решать 4-5 задач из ММОшных 6 (в спокойной обстановке), но из всероссийских мне давалась максимум половина (из последнего этапа). Замечу, что был «самоучкой» и занимался всегда сам, поэтому и не такой уровень, какой мог бы быть при более системном подходе.
Четыре мои основные книги, по которым я работал:
1. Задачник, автор Шарыгин, состоявший исключительно из школьных задач, но самых сложных.
Прорешав в начале 10 класса этот задачник, я обзавелся базовым уровнем, достаточным для понимания олимпиадных задач.
все про олимпиады школьников как искать, где готовиться, что писать. мой опыт и советы
2. Международные математические олимпиады, авторы Морозова и Петраков.
В первую очередь, эта книга ознакомила меня с ммо и его историей, что явлилось катализатором дальнейших моих усилий.
3. Зарубежные математические олимпиады, под редакцией Сергеева.
По этой книге я получил основное развитие в решении олимпиадных задач, в первую очередь функциональные уравнения, задачи на делимость, дифоантовы уравнения.
4. Двухтомник Прасолова — задачи по планиметрии.
К сожалению по нему я работал мало, поэтому не очень успешно справлялся с задачами по планиметрии, но насколько понял, в этом задачнике есть абсолютно все задачи, т.е. какая бы задача по планиметрии не попалась на ММО, она либо есть в этом учебнике, либо ее простая производная.
Мои мысли по подготовке к ММО (для успешного решенеия хотя бы 5 задач из 6). Во-первых, кол-во тем задач ограничено. И к некоторым темам можно подготовиться 100%. Отношу к ним неравенства и планиметрию (все приемы можно стандартизировать). Далее, это задачи на делимость и диофантовы уравнения (почти все приемы можно стандартизировать).
Ну и функциональные уравнения.
Я методы отрабатывал следующим образом: брал задачу, пытался ее решить на где-то час-два, если не получалась, разбирал решение и писал его вместе с книгой. Полностью осознавал и затем снова самостоятельно писал это решение. таким образом, метод становился «мой». Поначалу я вообще не пытался решить задачу, времени было мало и сразу ее «отрабатывал». Если задача получалась, я в любом случае смотрел в ответ и сличал их решение со своим, если оно различалось принципиально, то я усваивал их метод.
Чего я хочу добиться этой темой:
1. Составить конкретный набор методов-задач (и их последовательность), достаточных для успешной подготовки к различным олимпиадам с относительного нуля.
2. Все остальные нюансы.
КАК ПОДГОТОВИТЬСЯ К ОЛИМПИАДЕ?
По моему мнению, потенциальный олимпиадник должен пройти 3 этапа:
понимание — отработка — генерация.
Первый этап относитя к достижению уровня, достаточного для понимания олимпиадных задач, второй — это отработка различных методов, третье — умение увидеть эти методы в новых задачах, замаскированных составителями.
Буду благодарен помощи форумчан, например arqady смог бы, при желании, составить методичку подготовки к неравенствам и т.д.
Источник: dxdy.ru
8 ресурсов для подготовки к олимпиадам по математике от победителей
Своими фаворитами для подготовки к соревнованиям делятся математики: Георгий Вепрев, призер Международной математической олимпиады, и Михаил Иванов, победитель Международной математической олимпиады.
Георгий Вепрев
Агаханов Н. Х., Богданов И. И., Кожевников П. А., Подлипский О. К., Терешин Д. А. Всероссийская олимпиада школьников по математике 1993-2009. Сборник задач Всероссийской олимпиады (муниципального и заключительного туров) по математике с решениями.
Кохась К. П., Берлов С. Л., Власова Н.Ю., Петров Ф. В., Солынин А. А., Храбров А. И. Задачи Санкт-Петербургской олимпиады школьников. Каждый год выходит новая книга с задачами, решениями и статьями по олимпиадной математике.
Акопян А. В. Геометрия в картинках. Прекрасная книга для любителей геометрии. В ней собрано огромное количество задач, от совсем простых до очень сложных. Условие задачи представлено в виде картинки, так что можно решать и без бумажки.
Прасолов В. В. Задачи по планиметрии. Сборник задач по планиметрии. Геометрия на любой вкус, размер, и цвет.
Интернет-ресурсы
Art of Problem Solving. Здесь можно найти задачи со всего мира, поучаствовать в обсуждении, найти красивые решения.
Problems.ru. Огромный архив задач по всем темам на русском языке с решениями.
Михаил Иванов
Боревич З. И. Определители и матрицы. Хорошее пособие для тех, кто хочет познакомиться с началами линейной алгебры. Плюсом книги является правильная последовательность повествования: прежде чем ввести очередное понятие, автор мотивирует новое определение поучительными примерами.
Мельников О. И. Теория графов в занимательных задачах. С помощью этой книги можно значительно повысить навыки в сфере комбинаторных задач. Для каждой задачи указана сложность, а также приводится подробное решение. Эта книга помогла мне продвинуться в теории графов: как познакомится с парой новых комбинаторных приемов, так и попрактиковаться в решении непростых задач.
По моему мнению, олимпиады по математике отличаются от соревнований по другим предметам тем, что для подготовки к ним может быть достаточно очень активного участия в работе математического кружка. Необходимым условием успеха является регулярное решение задач (по геометрии, алгебре, теории чисел, комбинаторике; как простых, так и трудных), без которого простое чтение каких бы то ни было книг становится гораздо менее осмысленным.
Источник: 4ege.ru
Как хорошо написать олимпиаду по математике
Статья посвящена методическим аспектам разработки и проведения занятий по математике с обучающимися вузов при подготовке к Всеармейским олимпиадам. Авторами проведена серьезная работа по анализу олимпиадных задач по математике, представлена классификация задач по математическим разделам, раскрыта методика решения задач с позиций деятельностного подхода, даны рекомендации преподавателям по подготовке курсантов к олимпиаде. Отдельного внимания заслуживает представленная в статье совокупность задач по теме «Аналитическая геометрия», реализующая описываемую методику. Подобранная по данной теме совокупность задач направлена на формирование действий, необходимых для успешного решения олимпиадных задач. Практическая значимость исследования заключается в том, что разработанная методика проведения занятий с обучающимися может использоваться для подготовки курсантов к Всеармейским олимпиадам.
методика решения олимпиадных задач
классификация задач
обучение математике
1. Бочкарева О.В. Математические задачи как средство формирования профессиональных качеств личности / О.В. Бочкарева, Т.Ю. Новичкова, О.В. Снежкина, Р.А.
Ладин // Современные проблемы науки и образования. – 2014. – № 2. — URL: www.science-education.ru/116-12584.
2. Бочкарева О.В. Формирование профессиональных умений на занятиях по математике / О.В. Бочкарева, О.В. Снежкина, М.А. Сироткина // Молодой ученый. – 2014. – № 2 (61). – С. 735-738.
3. Гарькина И.А., Данилов А.М. Образовательная система с позиций идентификации и управления // Региональная архитектура и строительство. – 2013. – № 2 (16). – C. 143-147.
4. Гарькина И.А., Данилов А.М. Системный подход к повышению качества образования // Вестник КГУ им. Н.А. Некрасова. – 2013. – № 4. – Т. 19. – С. 4-7.
5. Ладин Р.А. Математика и междисциплинарные связи / Р.А. Ладин, О.В. Снежкина, О.В. Бочкарева, Н.В.
Титова // Молодой ученый. – 2014. – № 1. – С. 550-552.
6. Саранцев Г.И. Упражнения в обучении математике. — М. : Просвещение, 2005. – 256 с.
7. Сироткина М.А. К вопросу о профессиональной направленности обучения математике / М.А. Сироткина, О.В. Бочкарева, О.В. Снежкина // Вестник магистратуры. – 2014. – № 2 (29). – С. 59-61.
8. Снежкина О.В. О роли регионального компонента при преподавании дисциплин математического цикла / О.В. Снежкина, Г.А. Левова, О.В. Бочкарева, Р.А.
Ладин // Новый университет. Серия: Актуальные проблемы гуманитарных и общественных наук. – 2013. – № 11-12 (32-33). – С. 17-20.
Подготовка команды для участия во Всеармейской олимпиаде — длительный и трудоемкий процесс, который осуществляется в несколько этапов. На первом этапе проводится математическая олимпиада среди обучающихся института, по результатам которой осуществляется набор в группу подготовки к Всеармейской олимпиаде. Второй этап состоит в подготовке отобранных обучающихся по различным темам курса «Математика». К этим темам относятся следующие:
линейная алгебра;
аналитическая геометрия;
введение в математический анализ;
дифференциальное и интегральное исчисление;
дифференциальные уравнения;
Как известно из методической литературы, все задания курса «Высшая математика» подразделяются на четыре уровня.
Первый уровень. Для него характерно овладение отдельно взятым действием.
Третий уровень. Характеризуется овладением сложным действием, способностью применения этого действия вне алгоритмических ситуаций.
Очевидно, что задания для подготовки к олимпиаде принадлежат к четвертому уровню овладения действиями. Но и здесь следует выделить несколько видов заданий:
на свободное оперирование действиями, необходимыми для выполнения поставленной задачи;
на применение сложного действия вне алгоритмических ситуаций.
На примере темы «Аналитическая геометрия» поясним методику подбора задач для подготовки к олимпиаде.
Большинство задач по аналитической геометрии относятся к задачам второго вида, поэтому организация занятий по этой теме является одной из самых сложных. Нами разработаны занятия, которые позволяют классифицировать основные виды задач, предлагаемых на олимпиаде (как показал анализ олимпиадных заданий за последние несколько лет) [1; 2; 5].
Занятия по трем основным темам
На геометрическое место точек.
На угол между кривыми.
На кратчайшее расстояние между кривыми.
Завершением работы по теме «Аналитическая геометрия» является самостоятельная работа следующего содержания.
1. При каких значениях параметра k прямые
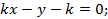
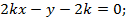
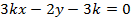
пересекаются в одной точке?
2. Найти угол между кривыми:
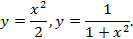
3. Найти кратчайшее расстояние между графиками функций:
, 
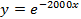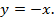
4. Один конец отрезка перемещается по оси абсцисс, а другой по оси ординат. Найти уравнение линии, описываемой серединой этого отрезка, если длина отрезка l.
5. Найти уравнение траектории точки М, которая движется так, что ее расстояние от точки А(-1;0) вдвое меньше расстояния до прямой х=-4.
Первая задача в самостоятельной работе относится к 1-му типу заданий, т.е. предполагает свободное оперирование действиями, необходимыми для ее решения.
Задачи 2-5, после проведенных занятий с обучающимися, должны из заданий 2-го вида для курсантов при решении стать задачами 1-го вида. Удачное выполнение самостоятельной работы будет свидетельствовать о том, что проведенные занятия цели достигли и обучающиеся свободно оперируют действиями, необходимыми для решения выделенных видов задач по теме «Аналитическая геометрия» [3; 4; 6].
Однако в последнее время наблюдается тенденция к расширению типов задач по теме «Аналитическая геометрия», выносимых на олимпиаду. В 2013 году тема «Аналитическая геометрия» рассматривалась совместно с темами «Определенный интеграл» и «Дифференциальные уравнения». Были выданы задачи следующего вида.
1. Из точек параболы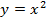 
проводятся касательные к параболе 
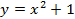. Доказать, что площадь криволинейного треугольника, образованного этими касательными и дугой параболы 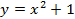между точками касания, не зависит от выбора точки на нижней параболе.
2. Составить дифференциальное уравнение парабол с осью, параллельной оси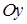 
, касающихся одновременно прямых 
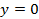и 
.
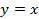Рассмотрим подробно решение каждой из задач и выделим моменты, на которые особо следует обратить внимание.
Первая задача связана с темой «Определенный интеграл», но для ее решения необходимо вспомнить уравнение касательной к кривой, проведенной в данной точке. Оно будет иметь вид:
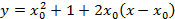
, (1)
где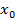 
, 
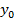– координаты точки касания. Поскольку касательная проходит через точку A( 
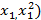параболы 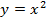то, подставляя ее координаты в уравнение (1), получаем
,
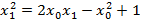
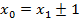
а значит, .
Далее переходим непосредственно к теме «Определенный интеграл» и вычисляем искомую площадь криволинейного треугольника ABC, вычитая из площади криволинейной трапеции MBCK, ограниченной параболой
,
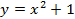
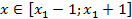, площади трапеций MBAN и NACK, ограниченных касательными и прямыми 
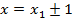(рис. 1).
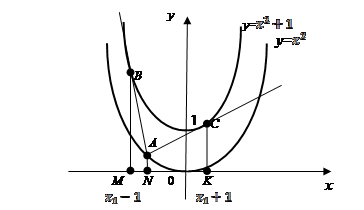
Рис. 1. Схема определения площади криволинейного треугольника ABC.
.
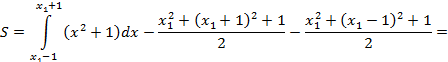
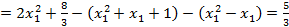
В итоге мы при вычислении интеграла получили число, а, следовательно, площадь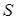 
не зависит от выбора точки 
.
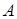При решении задачи следует актуализировать следующие знания из темы «Аналитическая геометрия»: уравнение касательной к кривой, площади трапеций [7; 8].
При решении второй задачи также необходимо уравнение касательной. Однако, наряду с уравнением касательной, необходимо иметь знания по каноническому уравнению параболы и особенностям этого канонического уравнения в зависимости от расположения кривой. Так, в задаче требуется составить уравнение семейства парабол с осью, параллельной оси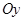 
.
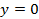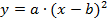
Это уравнение будет имеет вид . Для нахождения углового коэффициента касательной продифференцируем полученное уравнение:
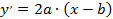
(2)
Далее опять же необходимы знания из темы «Аналитическая геометрия», а именно условие касания прямой 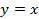вытекает, что 
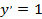. Этот факт с учётом формулы (2) даёт 
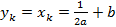, где 
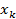и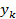 
– абсцисса и ордината точки касания соответственно. Отсюда, а также из формулы (2) следует, что:
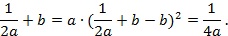
Из последнего равенства получаем
.
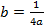
Подставив значение b в (2) , получим:
,
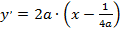
откуда найдем величину
.
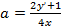
Подставив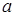 
и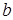 
в уравнение семейства парабол, получим:
,
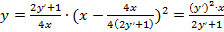
а после преобразований имеем искомое дифференциальное уравнение
.
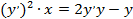
Таким образом, тема «Аналитическая геометрия» являлась в 2013 году базовой при решении задач по интегрированию функций и дифференциальным уравнениям. Особенно необходимы оказались знания по уравнениям касательных, проведенных к графику функций. Таким образом, выделенные в начале статьи типы задач, решаемых при подготовке к Всеармейским олимпиадам, а именно на нахождение угла между кривыми, послужат базой для успешного решения задач по другим разделам олимпиады.
Сама же тема «Аналитическая геометрия» была представлена в этом году следующими задачами.
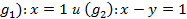
1. Составить уравнения сторон треугольника, зная одну из его вершин A(4;-1) и уравнения двух биссектрис (.
2. Вычислить радиус и координаты центра окружности
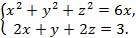
При решении первой задачи необходимо выполнить построение точки, симметричной вершине относительно биссектрисы треугольника. Такое построение никогда раньше нами при подготовке к олимпиаде не рассматривалось, поэтому требуется подбор типов задач на отработку данного действия.
Вторая задача включает в себя знания по взаимному расположению сферы и плоскости. Данный вид задач неоднократно решался при подготовке к олимпиаде, поэтому не является для наших обучающихся новым. Эти задачи включают в себя все основные знания по теме «Аналитическая геометрия» основного курса обучения: уравнение сферы, уравнение плоскости, расстояние от точки до плоскости, параметрические уравнения прямой, направляющий вектор прямой, нормальный вектор плоскости.
Таким образом, при подготовке к Всеармейским олимпиадам по теме «Дифференциальная геометрия» необходимо:
Отрабатывать типы задач, выделенные в начале статьи.
Уделять должное внимание самостоятельной работе обучающихся по отработке полученных знаний на практике.
Включить в план подготовки задачи, находящиеся на стыке нескольких тем курса «Высшая математика».
Включить в рассмотрение задачи, при решении которых используется понятие симметрии.
Рецензенты:
Найниш Л.А., д.п.н., профессор, зав. кафедрой «Начертательная геометрия и графика» ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г.Пенза.
Гарькина И.А., д.п.н., профессор, зам. зав. кафедрой «Математика и математическое моделирование», ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза.
Источник: science-education.ru