Чтобы хорошо решать математические задачи, нужно хорошо знать математику, и только? На самом деле всё не так однозначно. Математика — это не только умение хорошо считать, даже если речь о младших классах, но ещё и способность рассуждать логически, умение мыслить абстрактно и множество других навыков.
Создатели международной математической онлайн-олимпиады BRICSMATH.COM для учащихся 1–11-х классов, которая проходит на платформе «Учи.ру» до 13 декабря, готовы на конкретных примерах доказать, что математика — это всегда нечто большее. Попробуем решить несколько олимпиадных задач вместе с Сергеем Шашковым, специалистом «Учи.ру»?
Задача № 1. Переливалки
Есть задача на переливание, которая популярна в соцсетях. Условие звучит так: есть два ведра ёмкостью 3 литра и 5 литров и неограниченный запас воды. Как точно отмерить 4 литра?
В олимпиадной версии популярная задача переосмыслена. Сюжет немного другой: ёмкостей много, воду из них выливать нельзя, и нужно сделать так, чтобы во всех сосудах количество воды стало одинаковым.
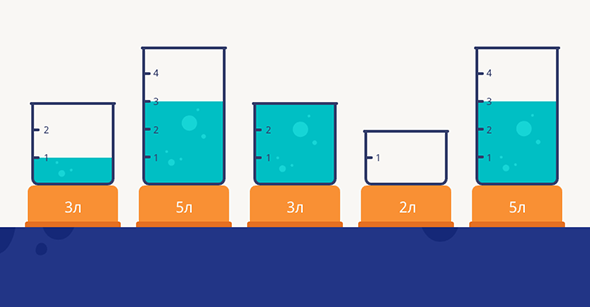
Начнём с того, что посчитаем суммарный объём воды во всех сосудах. Он не меняется и всё время составляет 1 + 3 + 3 + 3 = 10 л. Чтобы воды во всех сосудах было поровну, 10 литров нужно будет разделить на пять частей: получится по 2 литра в каждом сосуде. Значит, двухлитровый сосуд можно использовать как мерную ёмкость: можно по очереди опустошать очередной сосуд, затем наполнять двухлитровую ёмкость и переливать жидкость из неё в готовый пустой сосуд.
Задача № 2. Мария-путешественница
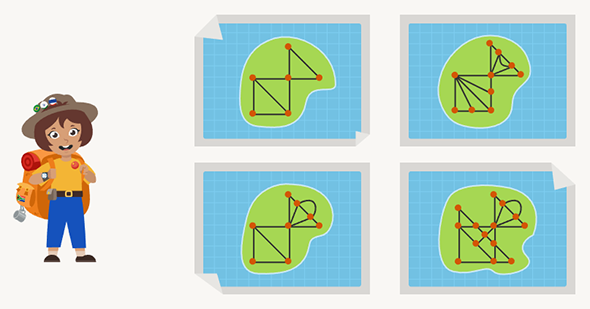
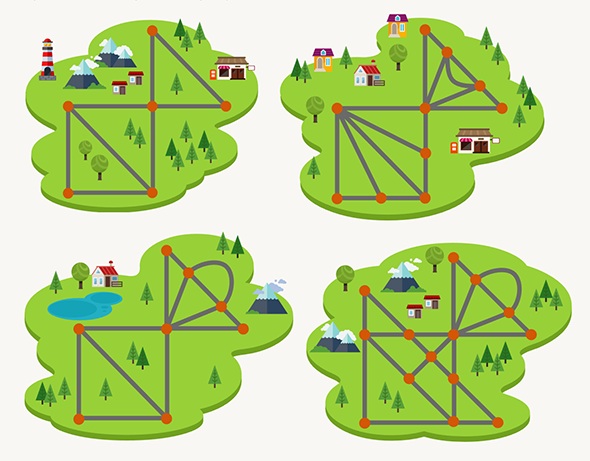
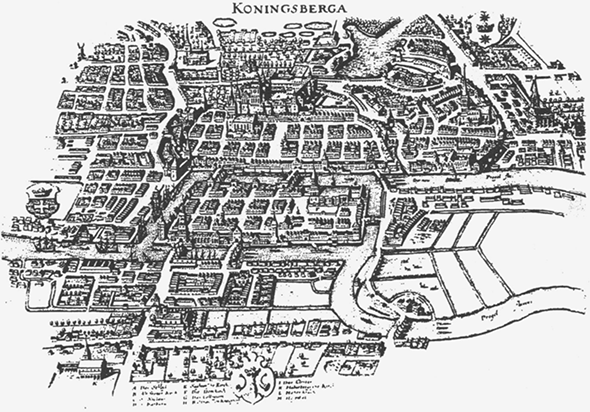
Эта детская олимпиадная задачка создана по мотивам известной задачи о семи кёнигсбергских мостах — старинной математической задачи о том, можно ли пройти по всем семи мостам Кёнигсберга, не проходя ни по одному из них дважды. Впервые она была решена в 1736 году математиком Леонардом Эйлером, который доказал, что так пройти по мостам нельзя. С тех пор пути, проходящие по всем мостам ровно по одному разу, называются эйлеровыми. А замкнутые пути — эйлеровыми циклами.
Вернёмся к Марии-путешественнице. Предположим, что она может прилететь в некоторую точку, после чего ей нужно будет обойти все дороги ровно по одному разу. Тогда входы-выходы из точек будут выглядеть так: вышла из первой точки, вошла-вышла, вошла-вышла, ещё несколько раз вошла-вышла, вошла и — ура, победа! Во всех точках, кроме первой и последней, вход и выход всегда идут парой.
Значит, в каждой точке, кроме старта и финиша, дороги должны разбиваться на пары. Если вдруг они не разбиваются хотя бы в трёх точках, то нужного пути найти не удастся. Это видно на примере ниже:
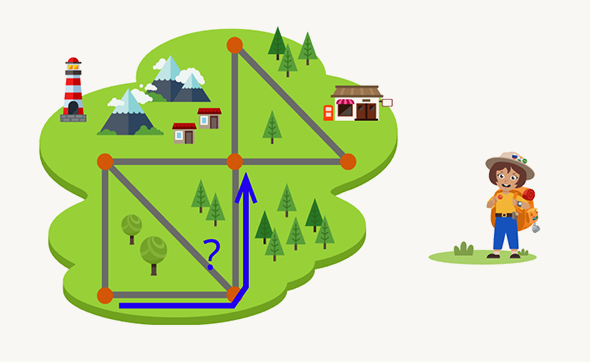
Допустим, что точек, в которых дороги не бьются на пары, всего две. Тогда нужно начинать путь из любой их них — путь всегда завершится во второй точке. Ещё может оказаться, что дороги бьются на пары в каждой точке. Этот случай оставим читателям, он приятно удивит.
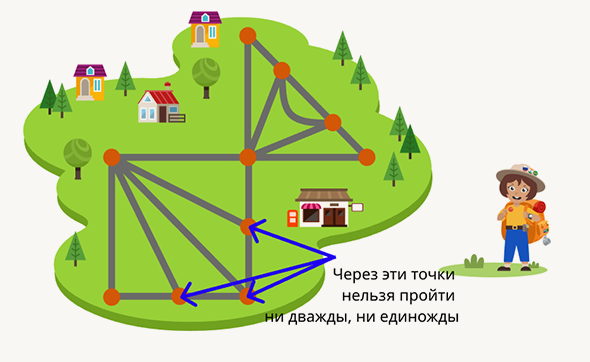
Кстати, математики называют подобные картинки графами, точки — вершинами, дороги — рёбрами. Число дорог, сходящихся в точке, называют степенью вершины. Но чтобы решить задачу про Машу-путешественницу, ребёнку не обязательно это знать: достаточно проявить смекалку и логику.
Задача № 3. Участок
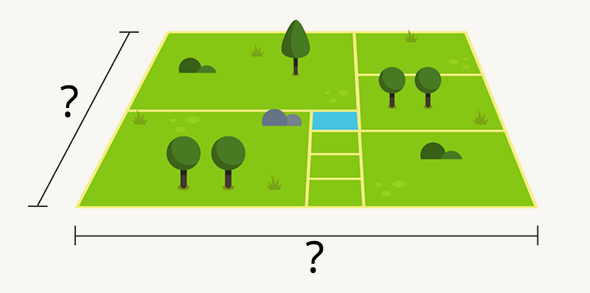
Эта задача для многих может показаться сложной. Кого-то пугает перспектива, а кто-то просто забывает, что у квадратов все стороны равны. Для решения достаточно знать это базовое правило и применить смекалку.
Если предположить, что размер пруда 1 × 1, то размеры каждого квадратика с общей с прудом стороной — тоже 1 × 1. Дальше эти квадраты можно использовать как линейку. Например, сразу получить размер левого нижнего квадрата — 4 × 4, или правого нижнего — 3 × 3. Так, двигаясь от соседа к соседу, можно получить стороны всех квадратов и решить задачу.
Олимпиада BRICSMATH.COM — бесплатное интеллектуальное соревнование по математике, которое проводится на базе онлайн-платформы «Учи.ру» для детей со всего мира. Задания олимпиады представлены в игровом формате и доступны на пяти языках. Поучаствовать можно до 13 декабря на сайте.
Онлайн-формат позволяет каждому ребёнку попробовать свои силы вне зависимости от уровня подготовки, социального и географического положения. Цель BRICSMATH.COM — не только популяризация математики и точных наук, развитие навыков логического мышления, но и объединение детей разных частей света в их стремлении к знаниям.
Источник: mel.fm
Способы решения олимпиадных задач по математике
Решение: всего в году 366 дней. Пусть дни будут «клетками», а ученики – «кроликами». Тогда в некоторой «клетке» сидят не меньше «кроликов», т.е. больше одного, отсюда следует, что не меньше двух.
2. Кот Базилио пообещал Буратино открыть великую тайну, если он составит чудесный квадрат 66 из чисел +1,-1,0 так, чтобы все суммы по строкам, по столбцам и по большим диагоналям были различны. Помогите Буратино.
Решение: Допустим, что квадрат составлен, тогда суммы чисел могут меняться в пределах от -6 до +6. Всего 13 значений. Строк в квадрате 6, столбцов 6, диагоналей 2. Получаем 14 различных сумм. Противоречие, значит составить такой квадрат невозможно.
3. На собеседовании пришли 65 школьников. Им предложили 3 контрольные работы. За каждую контрольную ставилась одна из оценок: 2,3,4 или 5. Верно ли, что найдутся два школьника, получившие одинаковые оценки на всех контрольных?
Решение: рассмотрим множество наборов из трех оценок за соответствующие контрольные. Количество таких наборов равно 43 или 64 (4 возможности за каждую из трех контрольных). Поскольку число учащихся больше 64, по принципу Дирихле каким-то двум учащимся соответствует один набор оценок.
2.2 Инвариант
Инвариант значит «неизменный».
Инвариантом некоторого преобразования называется величина или свойство, не изменяющееся при этом преобразовании. Главная трудность при решении задач на инварианты состоит в его поиске. Нахождение инварианта является самым важным шагом на пути к решению задачи.
В качестве инварианта чаще всего рассматриваются следующие способы решения олимпиадных задач:
• раскраска
• игры
«Вспомогательная раскраска»
Говорят, что фигура покрашена в несколько цветов, если каждой точке фигуры приписан определённый цвет. Бывают задачи, где раскраска уже дана, например, для шахматной доски, бывают задачи, где раскраску с данными свойствами нужно придумать, и бывают задачи, где раскраска используется как идея решения.
Суть данного метода состоит в следующем. Раскрасив некоторые ключевые элементы, которые фигурируют в задаче в несколько цветов, исследовать, что будет происходить, если выполнять условия задачи. Цвет позволяет значительно упростить понимание процесса, фигурируемого в условии, и зачастую приводит к решению. Этот метод позволяет эффективно решать ряд задач, в частности, игровые и шахматные задачи.
Задачи
1. Из шахматной доски вырезали две противоположные угловые клетки. Докажите, что оставшуюся фигуру нельзя разрезать на «домино» из двух клеток
Решение. Каждая фигура «домино» содержит одну белую и одну чёрную клетку. Но в нашей фигуре 32 чёрных и 30 белых клеток (или наоборот).
2. Можно ли все клетки доски 9 9 обойти конем по одному разу и вернуться в исходную клетку?
Решение. Каждым ходом конь меняет цвет клетки, поэтому, если существует обход, то число чёрных клеток равно числу белых, что неверно.
3. Дан куб 6 6 6. Найдите максимально возможное число параллелепипедов 4 1 1 (со сторонами параллельными сторонам куба), которые можно поместить в этот куб без пересечений.
Идея решения. Легко поместить 52 параллелепипеда внутрь куба. Докажем, что нельзя больше. Разобьем куб на 27 кубиков 2 2 2. Раскрасим их в шахматном порядке. При этом образуется 104 клетки одного цвета (белого) и 112 другого (чёрного).
Осталось заметить, что каждый параллелепипед содержит две чёрных и две белых клетки.
Ответ: 52.
4. Плоскость раскрашена в два цвета. Докажите, что найдутся две точки одного цвета, расстояние между которыми равно 1.
Решение. Рассмотрим равносторонний треугольник со стороной 1. По принципу Дирихле по крайней мере две из его трёх вершин должны быть покрашены в один цвет.
«Математические игры»
При изложении решения игровых задач школьники испытывают большие трудности. Ведь необходимо, во-первых, грамотно сформулировать стратегию, а во-вторых, доказать, что она действительно ведет к выигрышу. Поэтому задачи-игры очень полезны для развития разговорной математической культуры и четкого понимания того, что означает «решить задачу».
Под понятием математической игры мы понимаем игру двух соперников, обладающих следующим свойством. В каждый момент игры состояние характеризуется позицией, которая может изменяться только в зависимости от ходов игроков. Для каждого из игроков некоторые позиции объявляются выигрышными. Добиться выигрышной для себя позиции и есть цель каждого. Иногда игры допускают ничью.
Это означает, что ни один из игроков не может добиться выигрышной для него позиции, или некоторые позиции объявлены ничейными.
Например, шахматы, шашки, крестики-нолики являются математическими играми. А игры в кости, домино, большинство карточных игр математическими играми не являются, так как состояние игры зависит не только от ходов соперника, но и от расклада и результата бросания кости.
В математических играх существуют понятия выигрышной стратегии, т.е. набора правил (можно сказать, интуиции и алгоритма), следуя которым, один из игроков обязательно выиграет (независимо от того как играет его соперник), и ничейной стратегии, следуя которой один из игроков обязательно добьется либо выигрыша, либо ничьей. Например, крестики-нолики являются ничейной игрой. К какому из перечисленных случаев относится шахматы и шашки неизвестно.
Задачи
1.Двое кладут по очереди пятаки на круглый стол. Проигрывает тот, кто не сможет положить очередной пятак. Кто выигрывает?
Решение. Выигрывает первый. Он кладёт пятак в центр стола, после чего на любой ход второго у первого всегда есть симметричный ответ.
2. В куче 25 камней. Игроки берут по очереди 2, 4 и 7 камней. Проигрывает тот, у кого нет хода. Кто победит?
Идея решения. Случаи 0 и 1 камня проигрышны для начинающего. Поэтому случаи 2, 3, 4, 5, 7, 8 камней для начинающего выигрышны: своим ходом он переводит игру в позицию, проигрышную для противника. Аналогично, 6 и 9 камней проигрышны для начинающего, поскольку из них можно перейти только в позицию, выигрышную для противника. Рассуждая аналогично, легко установить периодичность выигрышных и проигрышных позиций и получить ответ.
3. Докажите, что в игре «крестики-нолики» на бесконечной доске у ноликов отсутствует выигрышная стратегия.
Решение. Пусть у ноликов есть выигрышная стратегия. Тогда этой стратегией могут с тем же успехом воспользоваться крестики, игнорируя свой начальный знак. (Когда крестикам приходится ходить на поле, где крестик уже стоит, они ходят куда угодно.)
Скачать Способы решения олимпиадных задач по математике
Ваш браузер должен поддерживать фреймы
Источник: ped-kopilka.ru
Подготовка к математическим олимпиадам. Общие сборники задач.
Можно ли самостоятельно подготовиться к классическим математическим олимпиадам? Можно, хотя для этого нужно будет много поработать. Конечно, хорошим подспорьем является наличие наставника или полноценного кружка с единомышленниками. Однако, при должной мотивации можно обойтись и без всего этого.
В этой мини-серии статей мы обсудим материалы для олимпиадников, которые хотели бы повысить свой уровень подготовки.
На что мы опирались, когда составляли эти подборки:
- Предполагается, что в школе у вас всё более-менее нормально с текущей программой. Может быть есть некоторые пробелы (а они есть абсолютно у всех школьников), но в целом в школьной математике вы себя чувствуете вполне уверенно.
- Мы учитывали то, что большинство из вас не специалисты олимпиадники, и поэтому постарались начинать с самых базовых вещей. Чуть ли не с 6-7 класса. Более сильные ученики могут сразу начать знакомиться с продвинутыми материалами, но всё равно для более эффективной работы лучше начинать с основ.
- Мы намеренно подбирали книги, которые удобны именно для самостоятельного изучения. В них даже сложные разделы объяснены вполне доступно. Наверняка, в кружках могут использовать методически более выверенные материалы, но там всё-таки есть преподаватель, который может всё объяснить, а в нашем случае мы будем считать, что такой возможности нет.
- Хотя списки получились довольно объёмными, мы уверены, что у каждого преподавателя найдётся ещё пара-тройка книг, которые он предпочёл бы в него добавить. Это нормальная ситуация. Мы имеем возможность редактировать статьи, поэтому при появлении новых достойных материалов мы можем их включить в рассмотрение.
- В подборке материалов делается упор именно на методы решения задач, а не на серьёзную фундаментальную проработку каких-то тем. Будет отдельная статья с материалами по внешкольной математике с более глубоким погружением в различные разделы математики. Желающие могут изучать темы параллельно.
- Мы не рассматривали олимпиадную элементарную геометрию. Про неё мы уже писали ранее в отдельных статьях.
- В этой первой части мы поговорим о сборниках задач, в которых затронуты основные темы олимпиадной математики. Во второй части мы обсудим книги, где каждая тема раскрыта по отдельности и более глубоко. Ну и наконец в третьей части мы обсудим различные сборники олимпиадных задач, которые позволят нам попрактиковаться в решении.
Итак, начнём со сборников, где вкратце затронуты основные темы из олимпиадной математики.
Школьные математические кружки (серия)
Это не книга, а подборка небольших брошюр, где доступным языком рассказываются основные подходы к решению задач в разных темах. Идеально подходит для начинающих. В них разобраны главные олимпиадные темы для учеников начиная с 6 класса: чётность, разрезания, инварианты, взвешивания, симметрия и пр.
Вертикальная математика для всех (Шаповалов А.В., Ященко И.В.)
На одной из закрытых конференций преподавателей к разработчику ЕГЭ по математике И.В. Ященко обратились с вопросом: “Cкажите, а как можно самостоятельно подготовиться к олимпиадной задаче из ЕГЭ?”. Он сказал, что достаточно только одной вот этой книги. Мы не согласны, что её будет достаточно, но по крайней мере прислушаться к его рекомендации можно. Книжка хорошая и также полезна для старта, особенно для старших классов.
Как решают нестандартные задачи (Канель-Белов А.Я., Ковальджи А.К)
Очень полезная книга, в которой описаны основные принципы решения олимпиадных задач. Книгу отличает от других то, что авторы стараются перед решением задач как можно больше исследовать их и посмотреть разные к ним подходы. И только после этого они объясняют применение методов решения на практике.
Принцип узких мест (Шаповалов А.В.)
Небольшая брошюра. Скорее нужна для быстрого вспоминания разных принципов решения олимпиадных задач.
Олимпиадный ковчег (Канель-Белов А.Я., Трепалин А.С., Ященко И.В.)
Хорошая подборка задач по классическим олимпиадным темам. Книга дополняет все выше перечисленные.
Следующие три книги уже для более серьёзного уровня подготовки, поэтому, чтобы получить от них пользу, можно параллельно знакомиться с материалами из второй статьи, где более глубоко разобраны конкретные олимпиадные темы.
Ленинградские математические кружки (Генкин С.А., Итенберг И.В., Фомин Д. В.)
Классика олимпиадной подготовки. Хорошо подходит для преподавателей и для самоподготовки учеников. Идеальна для крепких старшеклассников профильных классов.
Алгебра и теория чисел для математических школ (Алфутова Н. Б., Устинов А. В.)
Книга является базовой для олимпиадной подготовки в многих математических школах. Она довольно сложна для самостоятельного освоения и скорее подходит для продвинутых учеников. В конце этой книги есть невероятно подробный список источников, который позволит углубиться даже в самые узкие темы. Причём там указаны ссылки не только на книги, но и на различные статьи в журнале Квант.
Математика в задачах. Сборник материалов выездных школ команды Москвы на Всероссийскую математическую олимпиаду (коллектив авторов)
Как следует из названия, по этой книге готовят олимпиадников высокого уровня для выступления на заключительном этапе всероссийской олимпиады. В ней уже используются многие элементы из высшей математики. Книга будет также интересна тем, кто хочет связать свою судьбу с профессиональной математикой. Её можно рекомендовать только хорошо подготовленным ученикам, и, конечно, к ней желателен наставник высочайшего уровня математической подготовки, иначе вы можете просто испугаться сложности представленных примеров.
Эту книгу мы представили вам ещё и для того, чтобы вы видели, что нет предела совершенству и задачи могут всё усложняться и усложняться…
Источник: dzen.ru
