Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.
Деление столбиком — удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем — многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.
Запись чисел при делении столбиком
Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:
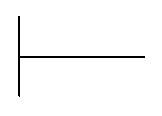
Деление столбиком на двузначное число. Простой способ деления на многозначное число.
Пусть нам нужно разделить 6105 на 55 , запишем:
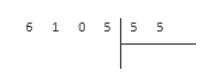
Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:
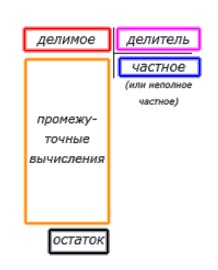
Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.
Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:
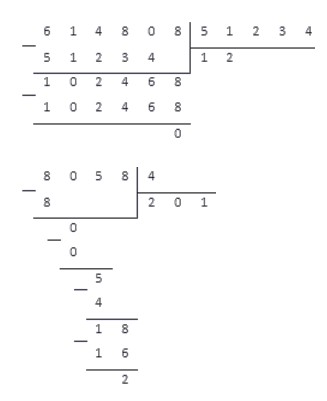
Деление столбиком на однозначное число
Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8 ÷ 2 = 4 .
Итак, сначала запишем делимое и делитель согласно методу деления в столбик.
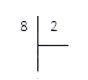
Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0 , 1 , 2 , 3 . . Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.
Деление на двузначное число в столбик. Как объяснить деление столбиком?
Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.
Вернемся к примеру.
2 · 0 = 0 ; 2 · 1 = 2 ; 2 · 2 = 4 ; 2 · 3 = 6 ; 2 · 4 = 8
Итак, мы сразу получили число, равное делимому. Записываем его под делимым, а число 4 , на которое мы умножали делитель, записываем на место частного.
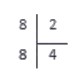
Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8 — 8 = 0 .
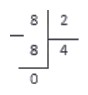
Данный пример — деление чисел без остатка. Число, получащееся после вычитания — это остаток деления. Если оно равно нулю, значит числа разделились без остатка.
Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3 .
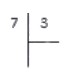
В данном случае, последовательно умножая тройку на 0 , 1 , 2 , 3 . . получаем в результате:
Под делимым записываем число , полученное на предпоследнем шаге. По делителем записываем число 2 — неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6 .
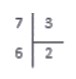
В завершение операции вычитаем 6 из 7 и получаем:
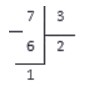
Данный пример — деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1 .
Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.
Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4 . Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.
Алгоритм деления столбиком
1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14 , так как первая цифра делимого 1 меньше, чем делитель 4 .

2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x = 14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ , включая нуль : 0 , 1 , 2 , 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x . Когда в результате умножения получается число 14 , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем. Если в результате умножения получается число, большее чем x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.
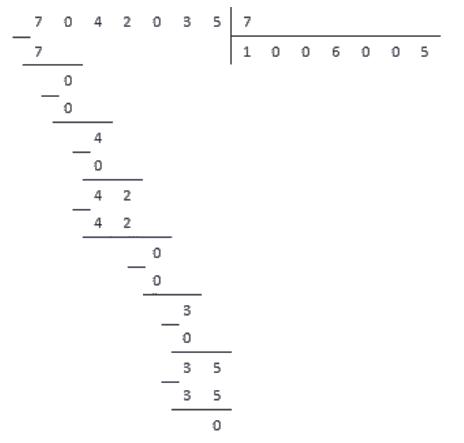
В соответствии с алгоритмом имеем:
Под выделенным числом записываем число 12 , полученное на предпоследнем шаге. На место частного записываем множитель 3 .

3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.

4. Число 2 меньше числа 4 , поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — 0 . В итоге отмечаем новое рабочее число — 20 .
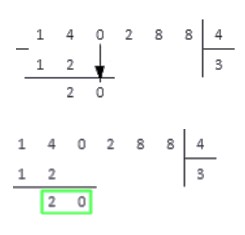
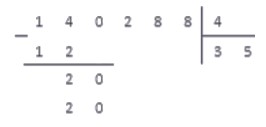
При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.
Деление многозначных натуральных чисел столбиком
Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2 — 4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе.Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Рассмотрим применение алгоритма деления многозначных чисел на примере.
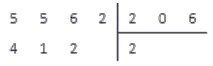
В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.
Источник: zaochnik.com
Доступно объясняем ребенку суть деления чисел. Деление в строчку и в столбик, а также двузначное на двузначное
Тема деления чисел в начальной школе является одной из самых сложных. Объяснить ее доступным языком можно и дошкольнику, однако учителя в школах часто отводят на объяснение недостаточно времени.
Они говорят, что деление — это действие, обратное умножению, важно лишь хорошо знать таблицу умножения. Деление в столбик они объясняют в первый раз на одном уроке, а дальше ребенок выполняет примеры сам, понял он эту тему или не понял. Программа на месте не стоит, нужно переходить к следующей теме, а то, что непонятно, как правило, так и останется непонятным для ребенка.
Эта статья для тех, кто как раз столкнулся с этой проблемой. Среди моих учеников такие есть:
— Деление двузначного числа на двузначное я не понял, учительница не объяснила это вообще. (Или ребенок эту тему проболел, а родители не смогли донести).
— Сколько бы ни делил в столбик, всё равно есть ошибки, и ничего не понято.
— Деление с остатком — вообще темный лес.
Объясняем суть деления на конфетах или деньгах
В любых случаях нужно объяснить ребенку для начала суть деления. Спросите его, знает ли он, что такое деление вообще? Если затрудняется с ответом, предложите ему поделить предметы: игрушки, конфеты, деньги.
— Вот есть 4 конфеты. Как сделать так, чтобы нам с тобой досталось поровну?
Ребенок с радостью отдаёт 2 конфеты и 2 остаются у него.
— Теперь разделим 9 рублей поровну между мной, тобой и бабушкой.
Ребенок может разложить монеты на столе на три кучки.
Всё, суть деления на наглядных предметах он понял. Далее надо переходить к числам. Записываем все эти примеры в числах, деньги и конфеты далеко не убираем. Пишем пример, например, 6 : 2, раскладываем при этом на столе 6 конфет, говорим, что надо разделить их между мамой и ребенком, то есть на два человека.
Мы объясняем наглядным способом, что первое число при делении показывает количество каких-то предметов, а второе число — на сколько человек мы эти предметы делим. Ответ показывает тоже предметы, но те, которые останутся у одного человека.
На этом этапе вводим понятия делимое, делитель, частное.
Делимое — число, которое делим (количество предметов в нашем случае).
Делитель — число, на которое делим (количество человек).
Частное — число, которое получается в ответе, результат деления (количество предметов у одного человека).
Таким образом показываем смысл деления наглядно, с опорой на доступные и понятные для ребенка предметы. Важно объяснить ему, что при делении всегда можно перейти на наглядные образы, если что-то не понял или забыл. Например, нужно ему поделить 21 на 3 в школе. Рядом нет игрушек и конфет, чтобы с их помощью разделить числа, но есть черновик, на котором можно нарисовать эти конфеты.
Я всегда прошу учеников рисовать в черновике кружочки, это якобы монеты. И делить их на кучки или группы, обводя некоторое количество. Получившиеся кучки — это делитель, то есть столько человек должны получить монетки.
От конфет и денег к примерам с числами
После предметного деления переходим к делению чисел без опоры на наглядность. Но её также можно продолжить использовать на черновике, если что-то непонятно.
На этом этапе нужно хорошо знать таблицу умножения . Если есть с ней проблемы, то сначала хорошо выучить. Без этого никуда, и деление без знания таблицы умножения выполнить невозможно.
Деление — это действие, обратное умножению.
Не нужно заучивать отдельно таблицу деления. Важно только рассуждать так:
Какое число надо умножить на 3, чтобы получилось 12? Вспоминаем таблицу умножения. Это число 4. Значит, 12 : 3 = 4.
Деление можно всегда проверить умножением.
Объясняем деление с остатком
Делать это нужно с опорой на наглядность на первом этапе. Дать ребенку 4 конфеты и попросить разделить их поровну между тремя членами семьи. Одна конфета остаётся, как мы её назовём?
Это остаток , который получается тогда, когда поровну разделить нельзя.
Записываем этот пример числами. 4 : 3= 1 (ост.1). Решаем несколько примеров и закрепляем эту тему.
Основная проблема учеников — это незнание, как вычислить остаток. Я обычно предлагаю делить так:
59 на 8 мы поделить не можем без остатка, а какое число можем? (Вспоминаем таблицу умножения). Можем 56 : 8 = 7. Теперь вычисляем остаток. Нужно просто от 59 отнять 56. Будет 3 — это и есть остаток. Проверяем, чтобы он был меньше делителя.
3 < 8. Решение верное.
Как сделать проверку? Деление всегда можно проверить умножением, а остаток просто сложить с ответом. Например:
Или по-другому: 7 • 8 + 3 = 59.
Объясняем деление двузначного на двузначное
Эта тема вызывает больше всего проблем в начальной школе. У ребят просто вылетает из головы способ деления. А делим мы способом подбора.
Например: 39 : 13 = ?
Пробуем в частном 2. Начинать рекомендуют всегда с двойки. 13 • 2 = 26. 26 не равно 39. Значит, 2 не подходит.
Пробуем 3. 13 • 3 = 39. Значит, 3 подходит. 39 : 13 = 3
Начинаем с 2. 21 • 2 — будет 84? Нет. 21 • 3 — будет 84? Нет. 21 • 4 — будет 84?
Да. Значит, 84 : 21 = 4.
Объясняем деление в столбик
Деление без остатка в столбик проводится строго по алгоритму, и ребенку его просто надо понять и запомнить. Другого более легкого объяснения не существует.
Источник: dzen.ru
Приём письменного деления многозначного числа на двузначное

На этом уроке будут разобраны два примера деления многозначных чисел на двузначные. Обычно для подбора пробной цифры мы заменяем делитель на круглое число. Но каким же долгим иногда бывает подбор пробной цифры! Решалочка предложила несколько иной подход к округлению делителя, если у него в разряде единиц стоит цифра 9.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет.
Получите невероятные возможности

1. Откройте доступ ко всем видеоурокам комплекта.

2. Раздавайте видеоуроки в личные кабинеты ученикам.

3. Смотрите статистику просмотра видеоуроков учениками.
Получить доступ
Конспект урока «Приём письменного деления многозначного числа на двузначное»

Сегодня мы с вами вновь займёмся делением. На этот раз делить будем многозначные числа на двузначные.
Вот, например, попробуем разделить пять тысяч четыреста девяносто четыре на шестьдесят семь. С чего мы начнём деление? В первую очередь определим первое неполное делимое и количество цифр в частном. Ни пять, ни пятьдесят четыре не могут быть первым неполным делимым, так как делитель, шестьдесят семь, больше этих чисел.
Значит, первое неполное делимое – пятьсот сорок девять десятков. И в частном будет две цифры.
Для того, чтобы проще было найти первую цифру частного, делим пятьсот сорок девять на шестьдесят. А так как шестьдесят – это произведение чисел десять и шесть, то мы пятьсот сорок девять сначала делим на десять, а потом пятьдесят четыре делим на шесть. Получается девять, но в частное мы эту цифру пока не записываем, так как она пробная. Перемножаем шестьдесят семь и девять.

Получается шестьсот три. Как хорошо, что девять мы не записали в частное! Ведь шестьсот три больше первого неполного делимого. А этого быть не должно. Но, если так случилось, надо вместо девяти в частном взять меньшее число. Возьмём в качестве пробной цифру восемь. Перемножаем её с делителем шестьдесят семь. Получилось пятьсот тридцать шесть.
Ну вот, другое дело. Это число меньше первого неполного делимого. Но мы ещё должны убедиться, что оно подобрано верно. Выполняем вычитание. Остаток равен тринадцати. Он меньше делителя.
Восьмёрка подходит. Записываем её в частное.
Следующее неполное делимое – сто тридцать четыре. Опять делим его на шестьдесят. Сначала на десять. А потом тринадцать делим на шесть. Пробная цифра – два. Перемножаем шестьдесят семь и два, получается сто тридцать четыре. Отлично, мы сразу подобрали нужную цифру.
Деление окончено. Частное равно восьмидесяти двум.
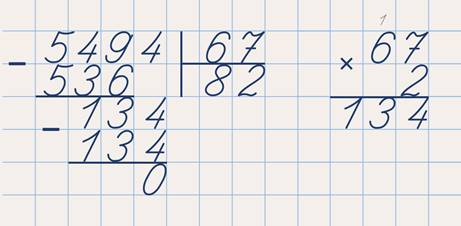
А теперь выполним деление чисел восемнадцать тысяч девятьсот четырнадцать и сорок девять.
Находим первое неполное делимое. Это сто восемьдесят девять. В частном будет три цифры. Сто восемьдесят девять делим на сорок, то есть сначала на десять. И восемнадцать делим на четыре.
Пробная цифра – четыре. Перемножаем сорок девять и четыре – получается сто девяносто шесть. Это больше, чем неполное делимое. Мда-а, многовато… Значит, четыре в частном не подходит. Попробуем три. Перемножаем с сорока девятью, получается сто сорок семь. А теперь не маловато ли? Сейчас проверим – вычтем его из ста восьмидесяти девяти.
Остаток – сорок два. Он меньше делителя, значит, три в частном – то, что надо. Это – количество сотен. Следующее неполное делимое – четыреста двадцать один. Если делить на сорок, то получится десять. Но этого просто не может быть, ведь в частное можно добавлять только по одной цифре от нуля до девяти.
Значит в качестве пробной возьмём цифру девять. Перемножаем с сорока девятью – получилось четыреста сорок один. Это число больше неполного делимого, поэтому и девять тоже не подходит. Возьмём пробную цифру восемь. Перемножаем с сорока девятью, получается триста девяносто два. Вычитаем его из четырёхсот двадцати одного.
Остаток – двадцать девять. Он меньше делителя, значит, количество десятков в частном мы нашли – их восемь. Третье неполное делимое – двести девяносто четыре. Делим его на сорок. Пробная цифра – семь.
Перемножаем семь и сорок девять, получается триста сорок три. Опять неудача, это число больше неполного делимого. Пробуем цифру шесть. Перемножаем с сорока девятью. Ура! Двести девяносто четыре.
В частном – шесть единиц. Деление окончено. Частное равно трёмстам восьмидесяти шести.
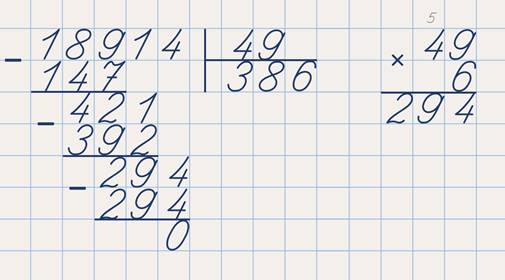
А вы знаете, ребята, о чём я сейчас подумала? Делитель в нашем примере – число сорок девять. Сорок девять – это почти пятьдесят, всего одной единички не хватает. А если бы мы делили не на сорок, а на пятьдесят? Давайте попробуем.
Первое неполное делимое, сто восемьдесят девять, делим на пятьдесят. Пробная цифра – три. Точно! Второе неполное делимое, четыреста двадцать один, делим на пятьдесят. Получается пробная цифра восемь. Опять верно.
Третье неполное делимое, двести девяносто четыре, делим на пятьдесят, получается пробная цифра пять. А вот тут должна быть другая цифра. Если мы умножим сорок девять на пять, получится двести сорок пять, и остаток будет равен делителю. Значит, пяти недостаточно. Надо взять шесть.
Видите, так тоже можно решить пример. И пробных чисел в частном получится меньше. Но этим способом удобно пользоваться в тех случаях, когда двузначный делитель оканчивается девяткой. Например, если делитель двадцать девять, можно попробовать делить не на двадцать, а на тридцать. А если делитель – семьдесят девять, можно попробовать делить не на семьдесят, а на восемьдесят.
Ну вот и подходит к концу наше занятие. Однако мне кажется, что надо проверить, внимательно ли вы меня слушали. Найдите частные в этой паре выражений:
33 366 : 67; 191 632 : 59
Проверьте своё решение.
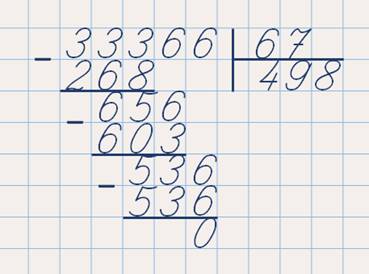
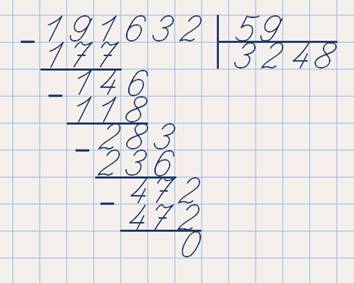
А теперь пришло время нам попрощаться. Удачного вам дня и до скорой встречи!
Источник: videouroki.net
