Как выполнить деление трёхзначного числа на однозначное число в столбик?
В отличие от письменного сложения, вычитания и умножения, деление начинают с единиц наибольшего разряда.
При делении в столбик очень важно правильно выполнять деление с остатком. Например:
25 : 4 = 6 ( ост . 1 ) .
Обрати внимание!
Остаток от деления чисел всегда меньше делителя!
Итак, разделим (714) на (3) в столбик.
Начинаем деление с разряда сотен.
(7) сотен делим на (3), получаем (2) сотни, их пишем в частном.
В остатке будет (1) сотня, её пишем под чертой.

К (1) сотне добавляем (1) десяток, вместе получаем (11) десятков ((1) сотня (= 10) десятков).
Делим десятки.
(11) десятков делим на (3), получаем (3) десятка, их пишем в частном.
В остатке будет (2) десятка , их пишем под чертой .

К (2) десяткам добавляем (4) единицы, вместе получаем (24) единицы.
Делим единицы.
(24) единицы делим на (3), получаем (8) единиц, их пишем в частном . Остаток — (0).
Получили частное (238) без остатка.
Источник: www.yaklass.ru
Деление столбиком на трехзначное число


На уроке познакомимся с делением на трехзначное число столбиком с остатком и без остатка, будем решать задачи с единицами площади, устроим небольшое соревнование на присуждения звания «Знаток математики».

План урока:
На уроке познакомимся с делением на трехзначное число столбиком с остатком и без остатка, будем решать задачи с единицами площади, устроим небольшое соревнование на присуждения звания «Знаток математики».
Начнем урок с разминки. Проверим, как вы знаете табличное деление! Ведь без знаний таблицы умножения и деления невозможно научиться делить столбиком на трехзначное число.
Примеры списывать не нужно. Записывайте только ответы в 4 столбика.

А теперь проверим ваши достижения. Сравните свои ответы с образцом. Ставьте карандашом +, если ответ верный, если же вы ошиблись, поставьте -.
Проверь себя.

Оцените свои достижения.

Письменное деление на трехзначное число
Ребята, как вы думаете, отличается ли алгоритм деления на трехзначное число от знакомого нам алгоритма на двузначное число?
Нет, не отличается! Давайте повторим последовательность наших действий при делении столбиком.

Используя данный алгоритм, решим вместе несколько примеров. Будем делать записи в черновике. Вы знаете, что цифры в частном – пробные, и требуется проверка.
984 : 123 1 155 : 9 318 : 106 5 850 : 9

Оставшиеся примеры на деление решите самостоятельно. Проверьте себя по образцу.
Проверь себя.

При делении многозначных чисел столбиком ребята часто пропускают нули в частном. Обидная ошибка! Как этого не допустить? Рассмотрим более сложные случаи деления, когда в частном появляются нули.

Есть маленькие секреты безошибочного деления столбиком!
- Обязательно определяйте количество цифр в частном. Даже если вы случайно пропустили нуль, точки подскажут, что цифр в частном недостаточно.
- Делайте проверку: умножьте делитель на частное. Должно получиться делимое.
А теперь решите самостоятельно пример. Подумайте, нужен ли нуль в частном. Сравните свое решение с образцом.
55 692 : 273
Проверь себя.

Деление на трехзначное число с остатком
Вспомним главное правило при делении с остатком.

Это правило применимо для деления на любое число (одно-, двух-, трехзначное и т.д.).
Ребята, перед вами тетрадь ученика 4 класса. Проверьте, как выполнено деление на трехзначное число с остатком. Решите эти примеры в своем черновике. Сравните. Оцените работу четвероклассника.

Во втором примере остаток 148 больше делителя 125. Как вы думаете, почему так получилось? Пробная цифра 2 не подходит. В частном должна быть цифра 3. Умножим 125 на 3. Получим 375. Остаток 23 меньше делителя 125.
А вот первый пример решен верно. Оставим его без изменений. Во втором примере исправим ошибку.

Решение задач с единицами площади

Ребята, взрослые люди часто испытывают досаду, занимаясь ремонтом дома или квартиры. Почему? Знакома ситуация, когда чуть-чуть не хватило краски или обоев? Нужно срочно бежать в магазин, чтобы купить недостающие материалы. Можно ли этого избежать?
Конечно, можно! Главное, правильно выполнить расчеты. Например, правильно измерить площадь пола под покраску или площадь стен под обои.
Задача

В комнате длиной 7 м и шириной 8 м укладывают на пол ламинат квадратами 50х50 см. Сколько штук ламината потребуется для этой комнаты?
Подсказка. Вычислите площадь комнаты и площадь одного квадрата ламината. Одинаковые ли единицы площади вы использовали? Выразите квадратные метры в квадратных сантиметрах.
Решите задачу самостоятельно.
Проверь себя.
S пола = 7 ∙ 8 = 56 (м²)
S лам. = 50 ∙50 = 2 500 (см²)
10 000 : 2 500 = 4 (шт.) – ламината в 1 м².
56 ∙ 4 = 224 (шт.) – ламината потребуется.
Ответ: 224 штук ламината.
Задача

Для покраски пола комнаты площадью 35 м² купили 3 кг краски. Хватит ли этой краски, если на 1 м² пола расходуется 100 г краски.
Выразим 3 кг в граммах.
35 ∙ 100 = 3 500 (г) – краски потребуется.
3 500 – 3000 = 500 (г) – краски не хватит для покраски пола.
Ответ: 500 г краски не хватит.
Решите аналогичную задачу самостоятельно и проверьте по образцу.
Задача
Стены комнаты решили оклеить обоями. Площадь поверхности составляет 80 м². На одной стене есть окно – 3 м², а на другой – дверь занимает 4 м². Хватит ли 7 рулонов обоев, если в одном рулоне 10 м² обоев.

Проверь себя.
3 + 4 = 7 (м²) – занимают окно и дверь.
80 – 7 = 73 (м²) – нужно оклеить обоями.
7 ∙ 10 = 70 (м²) – в семи рулонах.
73 – 70 = 3 (м²) – обоев не хватит.
Ответ: не хватит 3 м².
Ребята, на уроке мы учились делить на трехзначное число без остатка и с остатком, решали сложные задачи с единицами площади. А теперь настало время подвести итоги! Устроим небольшое соревнование на звание «Знатока математики».

Решите примеры за одну минуту!
(12 543 – 3 890 + 15 498) ∙ 69 ∙ 0 ∙594 =
640 ∙5 ∙0 +640 : 1 – 630 =
? + 150 – 240 – 10 + 26 = 526
Проверь себя.
Кому удалось справиться с заданием за одну минуту, может смело назвать себя большим молодцом!
В первом и втором выражениях самые наблюдательные заметили умножение на нуль (можно не вычислять все выражение, а ∙ 0 = 0).
В третьем выражении первое число можно быстро найти, вычисляя с конца обратным действием: 526 – 26 + 10 + 240 – 150 = 600
Источник: 100urokov.ru
Как умножать столбиком в 3 классе и в 4 классе

5 класс. Математика.
Автор Андрющенко Ольга Викторовна На чтение 6 мин. Просмотров 2.6k. Опубликовано 29 октября 2022
Рассмотрим в этой статье как умножать столбиком различные числа — двузначные, трехзначные и другие — большие и маленькие. Если умножать большие числа, то умножать их столбиком, конечно, быстрее и проще всего. Маленькие числа можно умножить и в уме. Рассмотрим умножение столбиком на примере. Умножать в столбик умеет уже и 3, и 4 класс.
Начинают вводить такой способ умножения уже в 3 классе, и закрепляют в 4 классе. То есть четвероклассник должен уметь это делать легко и быстро, а для этого надо хорошо знать таблицу умножения. А в 5 классе это уже отработанный навык. В этой статье мы дадим вам алгоритм умножения больших (начиная с двузначных) натуральных чисел и объясним как научить ребенка умножению, как правильно объяснить как считать в столбик.
В статье вы рассмотрите подробное решение примеров столбиком на умножение, повторите таблицу умножения и вспомните как решается любой пример на умножение больших чисел. Мы приведем примеры умножения в столбик натуральных чисел.
Умножение двузначных чисел столбиком
Умножим два числа: 25 и 44. Когда мы записываем числа столбиком, важно записать их друг под другом так, чтобы десятки были под десятками, единицы под единицами. Вот так считать в столбик:
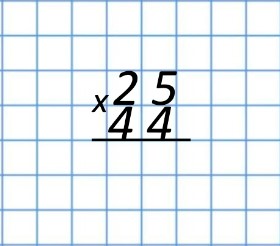
Теперь начинаем последовательно умножать сначала число 25 на первую четверку (число единиц), получим:

Обратите внимание — число 100 записывается в процессе умножения справа налево — то есть, идем от единиц к десяткам, умножаем сначала 5 на 4, получаем 20, записываем 0 под числом единиц, а число 2 держим в уме. Теперь умножаем 2 на 4, получаем 8, но так как у нас в уме еще 2, то складываем 2 и 8, получаем 10, записываем 10, причем так как мы сейчас умножаем число десятков на число единиц второго числа — на 4, то и число 10 записываем, начиная с числа десятков — 0 под десятками и 1 слева. В итоге получаем 100.
Мы умножили число 25 на число единиц 4 второго числа 44. Теперь сделаем умножение числа 25 на число десятков 4 числа 44. Результат умножения столбиком начнем писать справа налево, то есть начнем писать его под числом десятков, получим:
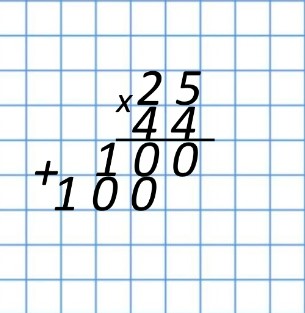
Итак, мы выполнили умножение числа 25 сначала на число единиц — 4 — второго числа 44, а потом на число десятков — 4 — второго числа 44. Следующим шагом будет сложение этих последовательных результатов умножения. Получим:
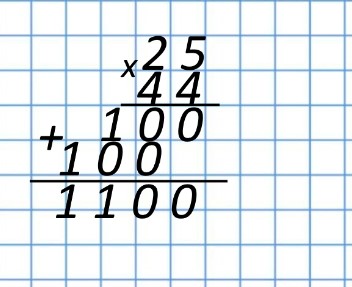
Обратите внимание — мы складываем не 100+100, а последовательно числа по разрядам, то есть сначала числа, стоящие на местах единиц (у нас тут один ноль), потом числа стоящие на местах десятков (0+0), числа, стоящие на позиции сотен (1+0) и числа, стоящие на месте тысяч (1). Если число только одно, то мы его просто сносим вниз, мысленно складывая с нулем.
Примеры умножения двузначных чисел
Чтобы лучше разобраться в умножении двузначных чисел столбиком, рассмотрим следующие примеры решения столбиком. Вы сможете рассмотрев каждый пример подробно научиться решать такие примеры:
Пример 1
Умножим число 15 на число 37. Пошаговый алгоритм умножения столбиком:

Пример 2
Умножим число 23 на число 79. Пошаговый алгоритм умножения столбиком:

Умножение столбиком трехзначных чисел
Для того, чтобы умножать столбиком трехзначные числа — все действия выполняем также, алгоритм не меняется. Только у нас появляется умножение первого (верхнего) числа на число сотен второго (нижнего) числа.
Давайте рассмотрим пример умножения столбиком трёхзначного числа на трехзначное число. Пусть нам нужно умножить 345 на 726. Вот что получится — пошаговый алгоритм:

Таким образом, общий принцип ясен и можно перемножать в столбик числа с любым количеством знаков.
Умножение столбиком многозначных натуральных чисел
Совет: Если вы умножаете первое число на число единиц (десятков, сотен, тысяч и далее) второго числа, число единиц произведения надо начинать записывать под числом единиц (десятков, сотен, тысяч и далее) второго числа.

Теперь рассмотрим, как надо умножать круглые числа. Тут есть небольшая хитрость для удобства умножения.
Умножение столбиком круглых чисел
Когда мы умножаем в уме круглые числа, мы не обращаем при умножении сначала внимания на ноль, например, нам нужно умножить 50 на 30. Мы в уме перемножаем 5 на 3 и просто приписываем два нуля, памятуя о том, что 10 на 10 дают 100.
Значит, если мы будем умножать, скажем 50 на 35, то эти числа в столбик нам удобнее записать не так:
Тогда нам нужно будет просто умножить число 35 на 5 и приписать 0. Здесь мы использовали следующее свойство умножения: от перемены мест множителей произведение не меняется. Поэтому вместо верхнего числа 50, мы записали нижнее число 35 — поменяли их местами.
Совет: чтобы проверить правильность умножения в столбик, вы можете поделить результат умножения на любой из множителей, если в результате деления без остатка вы получите второй множитель, значит, вы правильно умножили. Если деление произошло с остатком, значит, где-то была сделана ошибка. Деление тоже можно делать в столбик.
Итак, мы рассмотрели как умножать в столбик двузначные, трехзначные и любые многозначные натуральные числа, рассмотрели алгоритм умножения в столбик, привели примеры такого умножения.
Источник: mathematics-repetition.com
