На первый взгляд это простая задача про рыцарей и лжецов, но для ее решения понадобится знать несколько олимпиадных тем, принципов и идей.
На доске 4*4 в каждой клетке стоит либо рыцарь, либо лжец. И каждый из них говорит фразу «все мои соседи по стороне лжецы». Какое наибольшее количество лжецов может быть на этой доске?
На какую тему эта задача?
Когда я спрашиваю у детей, на какую тему эту задача, они единогласно отвечают, что рыцари и лжецы. Для решения задач на эту тему специфических знаний не нужно, но требуется понимать логическую структуру.
Если лжец говорит фразу «все мои соседи лжецы» и это ложь, то что тогда правда? Детям хочется ответить, что «все его соседи рыцари». Но это тоже вранье, потому что между утверждением и его отрицанием одно должно быть правдой, а второе — ложью. Это закон исключенного третьего.
А в нашей формулировке этот закон не выполняется. Как построить отрицание по законам логики? Отрицанием ко фразе «все мои соседи лжецы» будет «среди моих соседей есть хотя бы один рыцарь». Значит задача уже не только на тему рыцарей и лжецов, а на тему утверждений и отрицаний.
Какой принцип использовать?
Однако вопрос задачи состоит в подсчете наибольшего количества рыцарей. И ответ придется строить уже при помощи третьей темы: принцип рассуждения оценка плюс пример.
В задачах на наибольшее/наименьшее ответ состоит из трех частей:
- ⭐️предъявить ответ, например, 12 лжецов на доске;
- ⭐️показать размещение этих лжецов на доске;
- ⭐️и привести оценку, почему больше лжецов не влезает.
И если какой-то пункт в рассуждении отсутствует, то задача не считается решенной
⚡️Какие идеи подойдут?
Ну а чтобы привести оценку я советую использовать универсальные идеи, которые встречаются в самых разных задачах.
Идея первая — разбиение на фрагменты. В нашей задаче мы можем разбить доску на полоски или на квадраты 2*2. Разрезание на квадраты в нашей задаче подойдет лучше всего.
Идея вторая — рассуждать от угла. Угол — это узкое место, в наших квадратах 2*2 должно быть по 1 рыцарю, потому что если рыцаря нет, то угловой лжец говорит правду.
А для того, чтобы нарисовать пример, сработает моя любимая идея вентилятора , когда решение закручивается относительно центра. Давайте поставим рыцаря к стенке, но не в угол. А в остальных квадратах рыцарей закрутим вентилятором.
Источник: dzen.ru
Урок 27
§22. Логические задачи и способы их решения

Задачи о рыцарях и лжецах — это такой класс логических задач, в которых фигурируют персонажи:
• рыцарь — человек, всегда говорящий правду;
• лжец — человек, всегда говорящий ложь;
• обычный человек — человек, который в одних ситуациях может говорить правду, а в других — лгать.
Решение подобных задач сводится к перебору вариантов и исключению тех из них, которые приводят к противоречию.
Пример 2. Двое жителей острова А и В разговаривали между собой в саду. Проходивший мимо незнакомец спросил у А: «Вы рыцарь или лжец?». Тот ответил, но так неразборчиво, что незнакомец не смог ничего понять. Тогда незнакомец спросил у В: «Что сказал А?». «А сказал, что он лжец», — ответил В. Может ли незнакомец доверять ответу Б? Мог ли А сказать, что он лжец?
Если А — рыцарь, то он скажет правду и сообщит, что он рыцарь.
Если А — лжец, то он скроет правду и сообщит, что он рыцарь.
Это значит, что В, утверждающий, что «А сказал, что он лжец» заведомо лжёт; он — лжец. Определить же, кем является А, в данной ситуации невозможно.
Пример 3. Рядом стоят два города: город Лжецов (Л) и город Правдивых (П). В городе Лжецов живут лжецы, а в городе Правдивых — правдивые люди. Лжецы всегда лгут, а правдивые — всегда говорят правду. Лжецы и правдивые ходят друг к другу в гости.
Вы попали в один из городов, а в какой не знаете. Вам нужно у первого встречного, задав простой вопрос, узнать, в каком вы городе. Ответом на вопрос может быть только «Да» или « Нет ».
Нужен простой вопрос, ответ на который точно известен вашему респонденту. Например: «Вы находитесь в своём городе?».
Надо задать вопрос и проанализировать варианты ответов с учетом того, кто их мог дать.
Самостоятельно разберитесь с решением задачи, рассмотрев блок-схему на рис. 4.12.

Рис. 4.12. Блок-схема для анализа ответов
Пример 4. Перед нами три человека: А, В и С. Один из них рыцарь, другой — лжец, третий — нормальный человек. При этом неизвестно, кто есть кто. Эти люди утверждают следующее:
1) А: я нормальный человек;
2) В: это правда;
3) С: я не нормальный человек.
Кто такие А, В и С?
Для решения этой задачи следует рассмотреть все возможные варианты распределения ролей.
Начнём с А. Он может быть рыцарем (Р), лжецом (Л) или нормальным человеком (Н). Если А — рыцарь, то В может быть лжецом или нормальным человеком и т. д. Представим все варианты распределения ролей в таблице:

Проанализируем имеющиеся три утверждения, считая, что роли между А, В и С распределены в соответствии с первой строкой таблицы.
Итак, А утверждает, что он нормальный человек (1). Но, согласно первой строке таблицы, — он рыцарь, который не может так о себе сказать. Получено противоречие. Следовательно, первая строка не удовлетворяет условию задачи.
Самостоятельно проанализируйте оставшиеся строки таблицы и дайте ответ на вопрос, поставленный в задаче.

Cкачать материалы урока
Источник: xn—-7sbbfb7a7aej.xn--p1ai
Задача про рыцарей и лжецов
Задачи про рыцарей и лжецов — это классические математические задачи на комбинаторику.
Жили-были на одном небольшом островке в океане два племени — рыцари и лжецы. Рыцари были настолько горды и благородны, что не могли говорить ничего, кроме правды, правды и только правды. А лжецы не различали истину и вымысел.

На острове живут 50 человек. Из которых 35 — лжецы, 15 — рыцари. Какое наименьшее количество человек нужно выбрать, чтобы спросив потом у каждого, кто именно лжецы, по ответам вычислить хотя бы 1 лжеца?
Сразу поясню, что все жители острова знают, кто есть кто. И что отобрать людей для опроса нужно сразу, а не в зависимости от ответов, которые они дают.
Теперь начинаем рассуждать.
Когда мы спрашиваем жителя, кто рыцари, а кто лжецы, он указывает на 15 потенциальных рыцарей и 35 лжецов. Если спросить того, кого он назвал рыцарем, кто есть кто. То возможны 2 варианта:
- второй человек подтверждает версию первого (назовем их Команда 1)
- или его показания не сходятся с 1, а тогда значит, что врет либо второй (но первый назвал его рыцарем, а значит тоже соврал), либо первый. В любом случае мы идентифицируем 1 лжеца (первый). Ч и тд.
Допустим мы опросили 15 первых человек и все они — Команда 1. То есть абсолютно идентично называют себя рыцарями, а остальных — лжецами. Дает ли это право сказать, что мы решили задачу?
Не совсем. Они все могут оказаться лжецами, которые сговорились.
Теперь предположим что опросили 31 человека. Сепарировались Команда 1 (зеленые), Команда 2 (красные) и у нас 31-ый синий игрок, который называет рыцарем себя, а предыдущих 30 — лжецами. Кому довериться?

Могут быть правы, как первые, так и вторые, и даже 31-ый.
Опросим еще 5 человек. Если кто-то из новеньких 5 назовет рыцарями кого-то из красных или зеленых, то мы автоматически найдем 1 лжеца (тк красные и зеленые называют рыцарями только себя, а остальных — лжецами, а значит не может кто-то из 5 новеньких назвать рыцарем красно-зеленых).
Итак, все новенькие 5 называют рыцарями — синих.
Опросим 46 человек. И у нас будет 3 команды по 15 (зеленые, красные, синие) и 1 человек, который вроде как должен решить, кто же тут прав. Все 45 человек называли этого 46-го лжецом, значит он лжец, тк не собрал на свою сторону 15 человек.
А теперь развернемся. Вспомним, что ищем не того, кто прав. А ищем хотя бы одного лжеца. А значит, можно было остановить поиск намного раньше. Вот у нас 30 человек (красных и зеленых), которые ополчились друг против друга. Вот у нас 31-ый синий.
Должно получиться, что все 3 команды обзывают коричневых — лжецами. А коричневым будем не с кем объединиться, чтобы назвать своих 15 человек — рыцарями.
Но вдруг мы опросим еще 5 синих человек и выяснится, что первые 5 синих — говорят одно, а шестой синий назвался желтым и сказал, что все люди до него — врали.
Зеленые, красные, синие или жёлтые? Кто врет и где наш лжец?
Отгадка — в переметнувшемся синем. Остальные 5 синих назвали его своим, а он их предал, что означает, что синие — точно не рыцари. Иначе бы они знали, что переметнувшийся — лжец. И не называли бы его рыцарем. Мы всё еще не знаем, кто рыцарь — зеленые, красные или желтые, но синие — точно врут.
Вроде решили. Вот и я так подумала и отправила ответ.
Важным и ложным допущением было то, что мы делили группы на15 человек. А могло же быть по-другому. Команда 1 — 11 человек, команда 2 — 11, команда 3 — 11. итого 33 человека. Которые называют рыцарями себя и еще четверых, которые не вошли в первоначальную выборку для допроса.
Потом берем еще 11 человек — и они делают тоже самое (желтые).

Из оставшихся 6 коричневых есть 4 — которых все называют рыцарями. Кто врет — неизвестно. Продолжаем опрос.
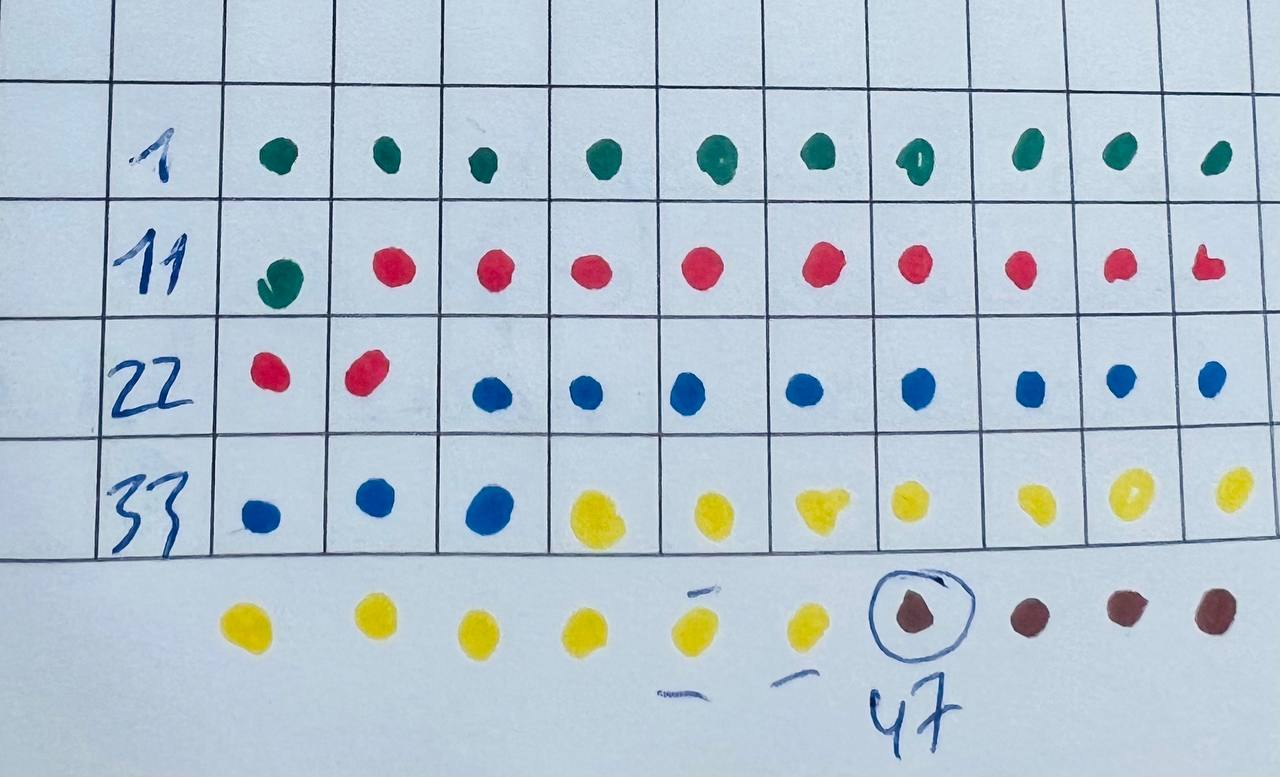
Берем еще 2 человека. Они должны будут присоединиться к одной из 4 фракций (зеленые, красные, синие, желтые). Допустим они выбрали желтых.
Тогда достаточно будет спросить 47 человека, которого все называют рыцарем (коричневый) и мы узнаем, где лжец. Даже сразу, где все лжецы. Тк 47ой человек — точно рыцарь.
Бонусом: немного другое толкование изначальных условий могло быть дать куда более интересное решение. Если бы можно было опрашивать островитян по очереди. То достаточно было бы спросить у пятерых, кто есть кто, и найти лжеца. То есть первый показывает на 15 рыцарей и 35 лжецов. Идем к лжецу.
Он указывает 15 своих рыцарей и обзывает лжецом первого и тд.
Но нет, нужно сразу взять рандомных людей и потом их опрашивать.
Также существуют целые классы задач того же типа, но с другими персонажами — задачи о пациентах и врачах, собранные в частности в книгах математика Рэймонда М. Смаллиана.
UPD
К сожалению, решение не поняли и принялись «с размаху» критиковать. Очень жаль.
Добавлю другое описание решения из учебника. Может быть сумею достучаться.
Источник: habr.com
