Какое самое маленькое число в математике

Ответ на вопрос в сканворде (кроссворде) «Наименьшее натуральное число», 7 букв (первая — е, последняя — а):

(ЕДИНИЦА) 0 0

Другие определения (вопросы) к слову «единица» (134)

1. Величина, которой измеряются другие однородные величины
2. Денежная …
3. Кол в тетради
4. Кол, «забитый» в дневник
5. Граница между бесконечностью целого и бесконечностью дробного
6. Отдельные предметы или люди, существа, немногие по числу
7. Неумножающий множитель
8. Товарищ нуля в двоичном коде
9. Оценка нулевых знаний
10. Знак двоичного кода
11. Абсолют дробного мира
12. Самая плохая оценка
13. Любое число в нулевой степени
14. «Боевая …»
15. Кол как школьная оценка
16. 1 женского рода
17. Часть целого
18. В математике: действительное число, от умножения на которое любое число не меняется
19. Наименьшее из натуральных чисел
20. Кол
21. Самая примитивная оценка в дневнике
22. Прима цифрового ряда
23. Нейтральный элемент относительно умножения
24. Не умножающий множитель (цифра)
25. Результат деления числа на самого себя
26. Низшая оценка в дневнике
27. Низшая оценка в российской школе
28. Число, на которое можно делить «без последствий»
29. Самое маленькое положительное нечетное число
30. Наименьшее положительное число
31. Оценка хуже двойки
32. Оценка шКОЛьная, весьма приКОЛьная
33. Оценка хуже некуда
34. Цифра, обозначающая число «1»
35. После неё двойка
36. В математике: действительное число
37. Наихудшая отметка
38. В математике: действительное число, от умножения на к-рое любое число не меняется
39. «Кол» в дневнике
40. Нижний предет нерадивости ученика
41. Худшая оценка в классе
42. Так называют величину, с помощью которой измеряются однородные величины
43. Название первого, наименьшего из натуральных чисел
44. Эталон арифметической стройности
45. Отметка хуже некуда
46. измерений
47. Лидер цифрового строя
48. (разг.) школьная отметка
49. В математике:действительное число,от умножения на которое любое число не меняется
50. Школьная отметка
51. Кол за контрольную
52. Школьная оценка – хуже некуда
53. Самая низкая оценка в школе
54. Начало отсчёта ученических оценок
55. Буква «е» в сокращении у. е
56. Школьный кол
57. … измерений
58. Самая низкая школьная отметка
59. Прекрасное зрение
60. На какое число без толку умножать
61. Отметка «кол» как число
62. Цифра
63. Одна пятая от отлично
64. Первый шаг арифметики
65. На какое число бесполезно делить
66. Отдельный предмет в группе подобных
67. «е» в «у.е.»
68. После неё идет двойка
69. Низшая оценка по пятибалльной шкале
70. Мнимая цифра
71. Мнимая …
72. Школьная оценка, привычная отличнику в Германии
73. Оценка для сверхленивых
74. Школьная отметка, похожая на колышек
75. Натуральный минимум
76. Школьная отметка (разг.)
77. Один из двух битов
78. Худшая школьная оценка, «кол»
79. Величина, к-рой измеряются другие однородные величины
80. Палочка в числе десять
81. Число 1
82. Цифра с носом
83. Самая плохая отметка
84. Палочка, без которой любая десятка – абсолютный ноль
85. На какое число бестолку умножать
86. Буква «Е» в сокращении «уе»
87. Позорнее двойки
88. «Один штук» товара
89. Штатная и боевая
90. Чему равно произведение взаимно обратных чисел?
91. Одна пятая «отлично»
92. Школьная отметка (разговорное)
93. Какая цифра, помимо нуля, используется в двоичной системе счисления?
94. Результат деления числа на само себя
95. Тангенс угла в 45 градусов
96. В Германии – «отлично», а у нас – кол
97. Произведение любого положительного целого числа на число ему обратное
98. Кол, в дневник забитый
99. Школьная оценка
100. Нижний предел нерадивости ученика
101. Первый разряд многозначных чисел
102. Величина, принятая за основу при измерении чего-либо
103. Кол, но не дубина
104. Число
105. Кол, но не дрын
106. Буква Е в сокращении у.е
107. Первое наименьшее из натуральных чисел
108. Кол, но не осиновый
109. Самая низкая отметка в российских школах
110. (разговорное) оценка успеваемости учащегося по пятибалльной системе, обозначающаяся цифрой «1» и соответствующая оценке «очень плохо»
111. Оценка ничего не знающего ученика
112. Отдельная самостоятельная часть в составе целого, отдельный предмет в группе подобных
113. Отдельная самостоятельная часть в составе целого, отдельный предмет (или человек) в группе подобных
114. Какая цифра, помимо нуля, используется в двоичной системе счисления
115. Штатная …
116. Вздор и ноль у Маяковского
117. Мера, стандартная величина
118. Мнимое число
119. … измерения
120. Не осиновый, но все же «кол»
121. Начало отсчета оценок ученика
122. Оценка для ничего не знающего ученика
123. «Кол» в дневнике школяра
124. Первая цифра при счёте
125. Самая низкая школьная учебная отметка
126. Величина, которой измеряются однородные величины
127. Самая позорная отметка
128. Штатная в штатном расписании
129. Оценка ниже двойки
130. Отдельная самостоятельная часть в составе целого
131. Самая редкая школьная отметка
132. Величина
133. Кол как оценка
134. Уже не ноль

Общее прототипическое значение — минимальное количество, минимальная величина для счёта чего-либо, кого-либо.

САМОЕ МАЛЕНЬКОЕ ЧИСЛО ЭТО НЕ 0❗️

Самое маленькое число. The smallest number.

1. + род. п. наименование величины, являющейся мерой для оценки других однородных величин ◆ Как единица массы, грамм есть одна из трёх основных единиц в системе абсолютных мер ( единица массы — грамм, единица длины — сантиметр, единица времени — секунда). A. Гершун, «Словарь Ф. А. Брокгауза и И. А. Ефрона // Грамм, единица веса и массы» ◆ Им были учтены каждый дом, каждый житель, каждая единица крупного рогатого скота, не говоря уже о реках, озёрах и ручьях, горах и долинах, видах деревьев и растений, животных и птиц и т. д. Л. В. Садовникова, «Агроном Иоганн Карл Эренфрид Кегель на Камчатке. 1841—1847 гг.», 2008 г.
2. матем. (математический термин) число, равное своему обратному; наименьшее положительное целое число
3. самостоятельная часть в составе какого-либо комплекса ◆ По словам самих казаков, станица Яйвинская была единственным подразделением среди российских казаков-добровольцев, которое как самостоятельная боевая единица сражалось в составе армии сербов. «Славянские народы. Русские», 28 декабря 2001 г. // «Жизнь национальностей» ◆ Иностранный филиал — это не имеющее статуса юридического лица подразделение банка за границей, то есть фактически структурная единица материнского банка. Андрей Верников, «Дочки страшные и не очень», 6 декабря 2004 г. // «Эксперт»
4. офиц. (официальное) штука, экземпляр ◆ Каждый день число коммерческих автобусов увеличивалось в среднем на три единицы . Максим Милованов, «Рынок тщеславия», 2000 г. ◆ Изъято 18 единиц оружия, в том числе три единицы огнестрельного. Олег Стулов, «Ведомости», 23 января 1996 г. // «Коммерсантъ-Daily»
5. школьн. (школьное) низшая отметка в учебных заведениях ряда стран, включая Россию ◆ Так же краснел и вздрагивал я, считая всё погибшим, когда получил единицу за физику и остался на втором курсе… Л. Н. Толстой, «Анна Каренина», 1878 г. ◆ Затем, обернувшись к сидевшему рядом с ним директору гимназии, он спросил вполголоса, не тот ли я ученик, который получил единицу по теоретической арифметике? Ю. П. Анненков, «Дневник моих встреч», 1966 г.

Значение слова

ЕДИНИ́ЦА, -ы, женский род

1. Первое, наименьшее целое число в десятке, а также цифра 1 (один), его обозначающая. || множественное число (едини́цы, -ни́ц). Последняя цифра многозначных чисел. [Мальчики] должны были писать мелом требуемые цифры и считать их —, повторяя: «единицы, десятки, сотни». С. Аксаков, Детские годы Багрова-внука.

2. Самая низкая оценка успеваемости в пятибалльной системе, означающая: 462 очень плохо; кол. Брат жены, Вася, тихо жует и угрюмо молчит, так как получил сегодня по латинскому языку единицу. Чехов, Сонная одурь.

3. Величина, принятая для измерения однородных с нею величин. Единица измерения. Денежная единица. ◆ Все эти потери переводятся на число баранов, служивших в то время как бы монетной единицей при денежных расчетах.

Семенов-Тян-Шанский, Путешествие в Тянь-Шань. [Петр Степанович] вышелушивал на ладонь зернышки, подсчитывал их, сбивался, снова начинал переводить в весовые единицы. Воронин, Братья.

4. Отдельное лицо, существо, предмет в группе подобных. Кутузов правильно говорит, что для каждой социальной единицы существует круг взглядов и мнений, химически сродных ей. М. Горький, Жизнь Клима Самгина. Не всматриваешься ты в лица И в душу не лезешь, — а все ж Для каждой людской единицы В таблицах ты место найдешь. Шефнер, Статистика.

[В годы войны] вчерашние буксиры и другие суда Северо-Западного речного пароходства стали боевыми единицами флотилии. Рупышев, Пахари моря. || множественное число (едини́цы, -ни́ц). Лишь некоторые, очень немногие лица. — И любовь, говорю вам, имеет свои вершины, доступные единицам из миллионов. Куприн, Поединок.

Писать так, как пишут формалисты, может всякий. Писать же как Тициан или рисовать как Александр Иванов могут только единицы. В. Яковлев, Художники, реставраторы, антиквары.

5. обычно с определением. Отдельная часть в составе целого, обладающая определенной самостоятельностью. Штатная единица. Хозяйственная единица. ◆ — Мы не учреждение и не заводоуправление, мы низовая производственная единица строительства, — доказывал Темкин. Ажаев, Далеко от Москвы.

Отряд Григорьева являлся как бы некоторой автономной и привилегированной единицей среди прочих частей гарнизона. Катаев, Записки о гражданской войне.

Едини́ца (един, оди́н) — многозначное слово.

Математика

• 1 (число) — целое число
• Единица группы — нейтральный элемент относительно групповой операции
• Единица (алгебра) — нейтральный элемент умножения в кольцах, полях, и алгебрах над ними
• Обратимый элемент: «группа единиц», «алгебраическая единица», и т.п.
• В теории множеств — см. кольцо (теория множеств)
• Мнимая единица

Источник: sinonim.org

Что такое натуральные числа

Сегодня мы расскажем, что такое НАТУРАЛЬНЫЕ ЧИСЛА.

С ними человек встречается с самого рождения. Например, когда считает пальцы на руке – 1, 2, 3, 4, 5. Или отмечает праздники – 8 марта, 23 февраля, 9 мая, 31 декабря.

Натуральные числа — это.

Натуральные числа – это те числа, которые возникают при подсчете чего-либо. Например, одно яблоко, два яблока, пять яблок десять яблок и так далее.

Лучше даже представить, что вы подсчитываете людей, ибо их нельзя поделить на части, как большинство предметов (например, разрезов яблоко пополам).

Само слово «naturalis» в переводе с латинского означает «естественный».

А вот если взять, к примеру, дробные числа (0.5, 13.856, 1/5 и так далее) и уж тем более отрицательные (-1, -5, -100), то в них весьма мало естественности. А значит, можно дать и другое, более простое определение натуральных чисел.

Если число не является ни дробным, ни отрицательным, то его можно назвать натуральным.

Натуральными числами люди пользуются уже много тысячелетий. Просто у разных народов были разные системы исчисления. Например, римляне для счета использовали палочки. Так и появились знаменитые римские цифры – I, V, X, L, C, D и M.

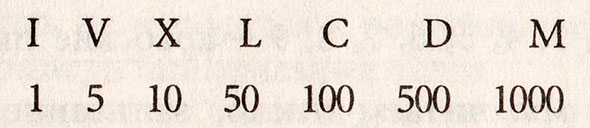
А вот в Древнем Вавилоне использовали шестеричную систему. И до наших дней она дошла в виде часов, в которых 1 час равен 60 минутам, а 1 минута равна 60 секундам.

И наконец, современное обозначение цифр (0, 1, 2, 3, 4, 5 и так далее) принадлежит арабам, хотя за основу они взяли индийскую десятеричную систему и добавили к ней «ноль».

Натуральный ряд

Если расположить натуральные числа в порядке возрастания, то полученная цепочка будет называться натуральным рядом.

Он всегда появляется, когда нам нужно что-то посчитать поштучно. Например, в магазине мы обычно так делаем с овощами или фруктами, берем 5 морковок или 3 яблока. А уже только потом взвешиваем их, так как цены указаны за килограмм.

И конечно, именно так учатся считать школьники в первом классе. Например, если в задачке нарисовано пять флажков и вопрос звучит «сколько?», то любой ребенок будет считать «пальцем», отмечая каждый флажок и озвучивая натуральный ряд «один, два, три, четыре, пять».

Ну и тут же будет важным упомянуть, что количество натуральных чисел бесконечно. А значит, и натуральный ряд является бесконечным.

Это записано в основном законе натуральных чисел:

Каким бы большим не было натуральное число N, всегда найдется натуральное число N+1, которое будет больше.

Ноль — это натуральное число или нет

Натуральный ряд можно построить двумя способами:

1. из чисел, которые обозначают нумерацию предметов (первый, второй, третий, четвертый и так далее);
2. из чисел, которые обозначают количество предметов (один, два, три, четыре и так далее).

Вы спросите, в чем разница? Во втором случае возможен вариант, когда нужного предмета может и не быть вовсе. И тогда его количество равно нулю.

То есть натуральный ряд начинается не с единицы, а с ноля. И выглядит вот так: 0, 1, 2, 3, 4, 5 и так далее.

Соответственно, в первом случае ноль нельзя считать натуральным числом. А во втором – можно. Интересно, что споры, какой подход более правильный, у математиков идут до сих пор. И сторонников обеих теорий примерно поровну.

Но у российских школьников проблем с выбором нет. В нашей стране придерживаются той версии, что ноль – это натуральное число.

Операции с натуральными числами

Школьники в младших классах на уроках математики имеют дело только с натуральными числами. Помимо самих цифр учатся и самым простым действиям:

1. Сложение. Слагаемое + Слагаемое = Сумма. И если слагаемые натуральные числа, то и сумма будет натуральным числом.
2. Вычитание. Уменьшаемое – Вычитаемое = Разность. Принцип натуральности чисел точно такой же.
3. Умножение. Множитель * Множитель = Произведение. При перемножении натуральных чисел получаем натуральное число.
4. Деление. Делимое / Делитель = Частное. В данном случае при делении натуральных чисел результат не обязательно должен быть натуральным числом. Возможен и дробный вариант. И еще главное правило – нельзя делить на ноль.

Вот и все, что мы хотели рассказать о натуральных числах.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

А стоит ли себе забивать голову, какое число натуральное, а какое нет? Мир от этого не станет, ни проще, ни сложнее. Да и что неестественного в отрицательных числах? Если человеку не хватает денег, чтобы рассчитаться с долгами, то его имущество как раз уйдет в минус, отдал за долги всё, что было, но остался должен, значит необходимо ещё заработать, чтоб из минуса выйти в ноль.

а нельзя сказать проще все недробные — натуральные?

Ваш комментарий или отзыв

Источник: ktonanovenkogo.ru

Натуральные числа

Множество натуральных чисел принято обозначать символом N (от лат. naturalis — естественный).

Существуют два исторических подхода к определению натуральных чисел:

• это числа, возникающие при подсчёте (нумерации) предметов (первый, второй, третий, …);
• это числа, возникающие при обозначении количества предметов (нет предметов, один предмет, два предмета, …).

Натуральные числа в десятичной системе счисления записываются с помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Множество натуральных чисел — является упорядоченным множеством, т.е. для любых натуральных чисел m и n справедливо одно из соотношений:

• либо m = n (m равно n),
• либо m > n (m больше n),
• либо m < n (m меньше n).

• Наименьшее натуральное число — единица ( 1 )
• Наибольшего натурального числа не существует
• Нуль ( 0 ) не является натуральным числом

Множество натуральных чисел бесконечно, так как для любого числа n всегда найдется число m, которое больше n.

Из соседних натуральных чисел, число, которое стоит левее числа n называется предыдущим числу n , а число, которое стоит правее называется следующим за n .

Операции над натуральными числами

К замкнутым операциям над натуральными числами (операциям в результате, которых получается натуральных чисел) относятся следующие арифметические операции:

• Сложение
• Умножение
• Возведение в степень a b , где a — основание степени и b — показатель степени. Если основание и показатель — натуральные числа, то и результат будет являться натуральным числом.

Дополнительно рассматривают ещё две операции. С формальной точки зрения они не являются операциями над натуральными числами, так как их результат не всегда будет натуральным числом.

• Вычитание (При этом Уменьшаемое должно быть больше Вычитаемого)
• Деление

Классы и разряды

Разряд — это положение (позиция) цифры в записи числа.

Низший разряд — самый правый. Старший разряд — самый левый.

Низший разряд — единицы, далее — десятки, сотни, тысячи, десятки тысяч, сотни тысяч, миллионы, десятки миллионов и т.д.

9 — единиц, 0 — десятков, 1 — сотя, 5 — тысяч, 3 — десятка тысяч, 4 — сотен тысяч, 2 — миллиона, 8 — десятков миллионов, 7 — сотен миллионов

Для удобства чтения, натуральных числа разбивают, на группы по три цифры в каждой начиная справа.

Класс — группа из трех цифр, на который разбито число, начиная справа. Последний класс может состоять из трех, двух или одной цифры.

• Первый класс — класс единиц;
• Второй класс — класс тысяч;
• Третий класс — класс миллионов;
• Четвертый класс — класс миллиардов;
• Пятый класс — класс триллионов;
• Шестой класс — класс квадриллионов;
• Седьмой класс — класс квинтиллионов;
• Восьмой класс — класс секстильонов;
• Девятый класс — класс септильонов.

Сравнение натуральных чисел

Сравнение натуральных чисел с разным количеством цифр

Среди натуральных чисел больше то, у которого больше цифр.

• 3466 > 346 , так как число 3466 состоит из 4 цифр, а число 346 из 3 цифр.
• 34666 < 245784 , так как число 34666 состоит из 5 цифр, а число 245784 из 6 цифр.

Сравнение натуральных чисел с равным количеством цифр

Сравнить числа поразрядно, начиная со старшего разряда. Больше то, у которого больше единиц в наивысшем одноименном разряде.

346 667 670 5 2 6 986
346 667 670 5 6 9 429

Второе из натуральных чисел с равным количеством цифр больше, так как 6 > 2 .

• Коротко о важном
• Таблицы
• Формулы
• Формулы по геометрии
• Теория по математике

1. Табличные значения синуса 30, 45, 60 градусов.
2. Минимум по геометрии 8 класса. Модуль 1.
3. Подготовка к контрольной работе по геометрии 8 класса.
4. Теорема о вписанном угле.
5. Сравнение скоростей снижения при прыжке с парашютом и прыжке из окна.

1. Таблица умножения (от 1 до 10).
2. Расширенная таблица умножения (от 1 до 20).
3. Таблица квадратов (от 1 до 10).
4. Таблица кубов (от 1 до 10).
5. Таблица степеней (от 1 до 10).
6. Таблица факториалов (от 1 до 10).
7. Таблица Брадиса (с уточнениями).
8. Как пользоваться таблицей Брадиса. Наглядная инструкция.
9. Таблица синусов.
10. Таблица косинусов.
11. Таблица тангенсов.
12. Таблица котангенсов.
13. Таблица тригонометрических функций.
14. Таблица значений функций.
15. Таблица натуральных логарифмов.
16. Таблица десятичных логарифмов.
17. Таблица логарифмов по основанию.

1. Формулы сокращённого умножения (2, 3, 4 и n-ой степеней).
2. Формулы и свойства степеней.
3. Формулы и свойства корней.
4. Формулы и свойства логарифмов.
5. Формулы и свойства арифметической прогрессии.
6. Формулы и свойства геометрической прогрессии.
7. Тригонометрические формулы.
8. Обратные тригонометрические функции.

1. Площади фигур.
2. Объёмы фигур.
3. Периметры фигур.
4. Площади поверхностей фигур.
5. Правильный многоугольник.
6. Треугольник.
7. Теорема Пифагора.

Источник: urokmatematiki.ru