Какой вклад в логику сделал евклид

Хотя Евклид — известный математик, о его жизни сведений сохранилось очень мало. Считается, что он был учеником Платона. Согласно данным из биографии, Евклид родился около 365 г. до н. э. в Александрии и умер до 265 г. до н. э. Самым известным произведением ученого является его коллекция из 13 книг, посвященных геометрии, под названием «Начала» (на латыни «Элементы»).

Жизнеописание

О годах жизни Евклида ничего не известно, кроме того, что греческий философ Прокл (ок. 410–485 гг.) изложил в своих описаниях древнегреческих математиков. По его словам, Евклид преподавал в Александрии во времена Птолемея I Сотера, который правил Египтом с 323 по 285 годы до нашей эры.

Средневековые переводчики и редакторы часто путали его с философом Евклидом из Мегары, современником Платона, жившим примерно за век до математика. Поэтому его иногда называли Мегаренсисом. Сегодня некоторые историки, изучающие биографию Евклида, оспаривают мнение, что этот ученый был старше Архимеда (ок. 290–212/211 до н. э.).

Пять постулатов Евклида.

В биографии Евклида говорится, что он собрал свой труд из ряда более ранних работ других ученых. Среди них Гиппократ Хиосский (расцвет научной деятельности — ок. 440 г. до н. э.), его не следует путать с врачом Гиппократом Коса (ок. 460–375 гг. до н. э.).

Последним компилятором был Теудий из Магнезии, учебник которого использовался в Академии и, вероятно, был тем, который использовал Аристотель (384–322 гг. до н. э.). Старые «Элементы» были немедленно заменены трудом Евклида, а затем забыты. Несмотря на то что это по большей части компиляция, ученый и сам много сделал для его написания, а кульминацией работы стало построение пяти регулярных тел, теперь известных как платоновы тела.

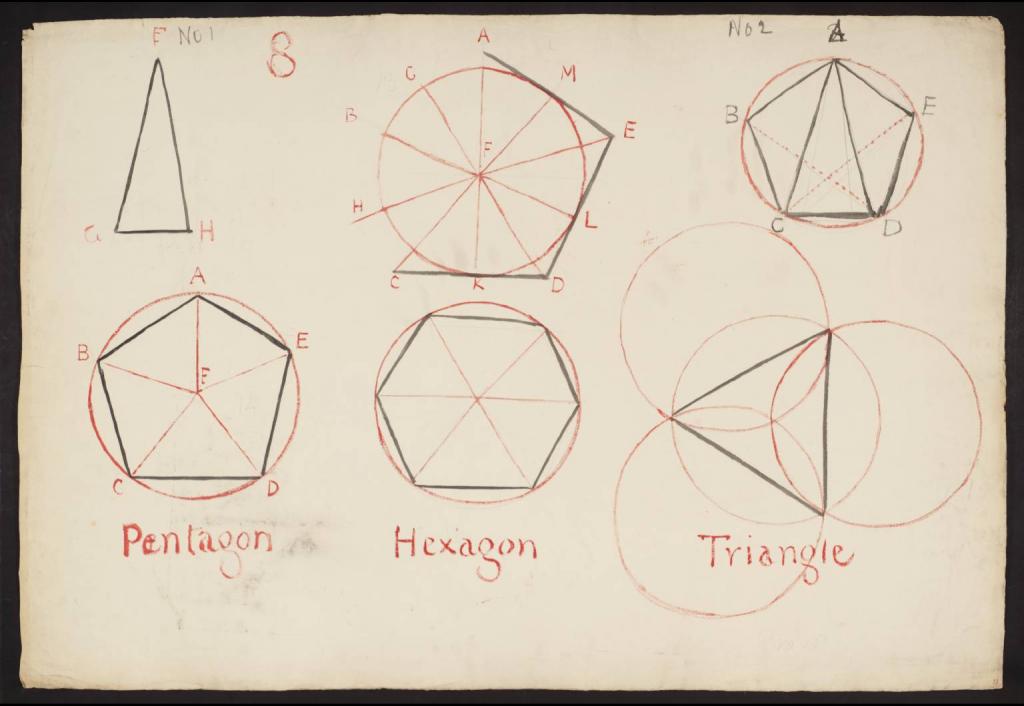
Краткий обзор

Вопреки общему убеждению, «Начала» Евклида касаются не только геометрии. Это неправильное представление может быть вызвано чтением лишь Книг I-IV, не далее, которые охватывают элементарную геометрию плоскости. Евклид понимал, что построение логической и четкой геометрии (и математики) зависит от основы, которую он представил в Книге I с 23 определениями (например, «точка — это то, что не имеет части» и «линия — это длина без ширины»): пять недоказанных предположений, которые он назвал постулатами (теперь известные как аксиомы), и пять дополнительных недоказанных предположений, которые он назвал общими понятиями. Затем Книга I доказывает элементарные теоремы о треугольниках и параллелограммах и заканчивается теоремой Пифагора.

Аксиомы

1. Между двумя точками можно провести прямую.
2. Сегмент прямой может быть продлен до бесконечности.
3. Круг можно построить, если указать точку для его центра и расстояние для его радиуса.
4. Все прямые углы равны.
5. Если прямая линия, падающая на две прямые линии, образует внутренние углы с одной и той же стороны меньше двух прямых углов, две прямые линии, если они образуются неопределенно долго, встречаются на той стороне, на которой углы меньше двух прямых углов.

Общие понятия

1. Вещи, равные одному и тому же, равны.
2. Если равные добавляются к равным, целые будут равны.
3. Если равные вычитаются из равных, оставшиеся будут равны.
4. Совпадающие друг с другом равны.
5. Целое больше части.

Евклид

Предмет Книги II был назван геометрической алгеброй, потому что в нем утверждаются алгебраические тождества как теоремы об эквивалентных геометрических фигурах. Книга II содержит конструкцию «сечения», деления линии на две части, так что отношение большего к меньшему сегменту равно отношению исходной линии к большему сегменту (это разделение в эпоху Возрождения было переименовано в золотое сечение, после того как художники и архитекторы заново открыли его пропорции). Книга II также обобщает теорему Пифагора. В Книге III рассматриваются свойства окружностей, а в Книге IV — построение правильных многоугольников, в частности пятиугольника.

Книга V переходит от плоской геометрии к изложению общей теории отношений и пропорций, которая приписывается Проклом (наряду с Книгой XII) Евдоксу Книдскому (ок. 395/390–342/337 до н. э.). Хотя Книгу V можно читать независимо от остальных частей «Начал», ее решение проблемы несоизмеримости (иррациональных чисел) имеет важное значение для более поздних книг. Кроме того, она легла в основу геометрической теории чисел, пока в конце 19-го века не была разработана аналитическая теория. Книга VI применяет эту теорию отношений к плоской геометрии, главным образом треугольникам и параллелограммам, кульминацией которой является «применение областей», процедура решения квадратичных задач геометрическими средствами.

Книги VII–IX

Они содержат элементы теории чисел, где число (арифмос) означает положительные целые числа больше 1. Начиная с 22 новых определений, таких как «единство, четное, нечетное и простое число», эти книги развивают различные свойства положительных целых чисел. Например, в Книге VII описывается метод антареоза (теперь известный как алгоритм Евклида) для нахождения наибольшего общего делителя двух или более чисел. В книге X также есть его описание. Алгоритм Евклида считается самым старым из тех, которые используются в наши дни.

В книге VIII рассматриваются числа в непрерывных пропорциях, которые теперь называются геометрическими последовательностями (такими как ax, ax 2 , ax 3 , ax 4 . ); и Книга IX доказывает, что существует бесконечное множество простых чисел.

Согласно Проклу, Книги X и XIII включают работы Теэтета Пифагорейского (ок. 417–369 гг. до н. э.). Книга X, которая составляет примерно одну четвертую всех «Начал», кажется непропорциональной по отношению к важности ее классификации несоизмеримых линий и областей (изучение этой книги вдохновило Иоганна Кеплера (1571–1630) на поиск космологической модели).

Книги XI–XIII

В них ученый исследует трехмерные фигуры в греческой стереометрии. Книга XI касается пересечений плоскостей, линий и параллелепипедов (твердые тела с параллельными параллелограммами в качестве противоположных граней). В книге XII применяется метод исчерпывания Евдокса для доказательства того, что области кругов расположены друг относительно друга как квадраты их диаметров, а объемы сфер соответствуют друг другу как кубы их диаметров. Кульминацией книги XIII является построение пяти правильных платоновых тел (пирамида, куб, октаэдр, додекаэдр, икосаэдр).

Неравномерность нескольких книг и различные математические уровни могут создать впечатление, что Евклид был всего лишь редактором трактатов, написанных другими математиками. В некоторой степени это, безусловно, верно, хотя, вероятно, невозможно определить, какие части являются его собственными, а какие были адаптациями его предшественников. Современники древнегреческого математика Евклида считали его работу окончательной и авторитетной.

Влияние

В древние времена комментарии были написаны Героном Александрийским (ок. 62 г. н. э.), Паппусом Александрийским (ок. 320 г. н. э.), Проклом и Симплицием Киликийским (ок. 530 г. н. э.). Теон Александрийский (ок.

335–405 гг. до н. э.) отредактировал «Начала» Евклида, внеся текстовые изменения и некоторые дополнения; его версия быстро вытеснила другие издания, и она оставалась греческим источником для всех последующих арабских и латинских переводов до 1808 года, когда в Ватикане было обнаружено более раннее издание.

Огромное влияние этого труда на исламскую математику заметно по многочисленным переводам на арабский язык начиная с 9-го века, три из которых должны быть упомянуты: два перевода сделал аль-Хаджадж ибн Юсуф ибн Махар, первый для аббазидского халифа Харуна аль-Рашида (правил в 786–809 гг.) и для халифа аль-Магмуна (правил в 813–833 гг.); и третий — Исак ибн Шунайн (умер в 910 году), сын Шунайна ибн Искака (808–873 гг.), который был пересмотрен Тхабитом ибн Куррой (ок. 836–901 гг.), а затем Насиром аль-Дином Сусси (1201–1974 гг.). Ученый Евклид впервые стал известен в Европе благодаря латинским переводам этих версий.

Первый существующий латинский перевод «Начал» был сделан около 1120 года Аделардом Батским, который получил копию арабской версии в Испании, куда он путешествовал, будучи замаскированным под студента-мусульманина. Аделард также составил сокращенную версию и издание с комментариями, положив тем самым евклидову традицию, имеющую огромное значение, пока в период Ренессанса не обнаружили греческие рукописи. Бесспорно, лучший латинский перевод с арабского языка был сделан Жераром из Кремоны (с. 1114-87) по версии Исхак-Сабита.

Первый прямой перевод с греческого был сделан Бартоломео Замберти и опубликован в Вене на латыни в 1505 году, а первое издание греческого текста было опубликовано в Базеле в 1533 году Симоном Гринеем. Первый английский перевод книг был сделан сэром Генри Биллингсли в 1570 году. Воздействие этой деятельности на европейскую математику не может быть преувеличено; идеи и методы Кеплера, Пьера де Ферма (1601–1665 гг.), Рене Декарта (1596–1650 гг.) и Исаака Ньютона (1642 –1727 гг.) корнями уходят в «Начала» Евклида и были немыслимы без них.

Другие сочинения

Евклидов корпус состоит из двух групп: элементарной геометрии и общей математики. Хотя многие средневековые труды Евклида были переведены на арабский язык, произведения обеих групп исчезли. В первой группе сохранились «Данные» (от первого греческого слова в книге: dedomena — «дано»), разнородная коллекция из 94 расширенных геометрических предложений, которые принимают следующую форму: задан некоторый элемент или свойство, затем другие элементы или свойства также «даны», то есть они могут быть определены. Некоторые из предложений можно рассматривать как упражнения по геометрии, чтобы определить, можно ли построить фигуру евклидовыми средствами.

Четыре утраченные работы по геометрии описаны в греческих источниках и приписаны Евклиду. По словам Прокла, цель «Псевдологии» («Заблуждения») состояла в том, чтобы отличить и предупредить новичков от различных типов заблуждений, которым они могут быть подвержены геометрическими рассуждениями. По словам Паппуса, «Поризмы» («следствия») в трех книгах содержали 171 предложение. Мишель Каслес (1793–1880) предположил, что в работе содержатся положения, принадлежащие современной теории трансверсалей и проективной геометрии.

Среди сохранившихся работ Евклида — «Оптика», первый греческий трактат о перспективе, и «Феномен» — введение в математическую астрономию. Эти работы являются частью корпуса, известного как «Маленькая астрономия», который также включает в себя «Подвижную сферу» Автолика Питана.

Два трактата о музыке, «Подразделение шкал» (в основном пифагорейская теория музыки) и «Введение в гармонию», когда-то ошибочно считались «Элементами музыки» — утраченной работой, приписанной Проклом Евклиду.

Вклад в науку

Почти со времени написания его основной труд оказывал постоянное и значительное влияние. Это был основной источник геометрических рассуждений, теорем и методов, по крайней мере, до появления неевклидовой геометрии в 19-м веке. Иногда говорят, что, помимо Библии, «Начала» являются самыми часто переводимыми, публикуемыми и изучаемыми из всех книг, выпущенных в западном мире. Если исходить из его биографии, Евклид, возможно, не был первоклассным математиком, но он установил стандарт для дедуктивного мышления и геометрического обучения, который сохранялся практически без изменений в течение более 2000 лет.

Источник: nacion.ru

Евклид

Древнегреческий мыслитель Евклид стал первым математиком Александрийской школы и автором одного из наиболее древних теоретических математических трактатов. О биографии этого ученого известно намного меньше, чем о его работах. Так, в известном труде «Начала» Евклид изложил стереометрию, планиметрию, аспекты теории чисел, создал базу для последующего развития математики.

Биография Евклида предположительно началась в 325 году до нашей эры (это примерная дата, точный год рождения неизвестен) в Александрии. Некоторые исследователи предполагают, что будущий математик появился на свет в Тире, а большую часть взрослой жизни провел в Дамаске. Вероятно, Евклид происходил из богатой семьи, так как он учился в афинской школе Платона (на то время такое образование было доступно только состоятельным гражданам).

Ученым удалось установить, что автор «Начал» был моложе известных последователей Платона, живших и творивших в период с 427 по 347 века до нашей эры, однако старше Архимеда, родившегося в 287 году и скончавшегося в 212 году до нашей эры. Евклид разбирался в философской концепции Платона и разделял ее основные положения.

Приведенная выше информация о личности и жизненном пути Евклида почерпнута исследователями из комментариев Прокла, написанных им к первой книге «Начала». Также известны высказывания Стобея и Паппа о личности древнегреческого мыслителя. Стобей якобы рассказывал, что в ответ на вопрос ученика о выгоде от науки Евклид приказал рабу выдать ему несколько монет. Папп же отмечал, что ученый умел быть любезным и мягким с любым человеком, который мог хоть в какой-то степени быть полезным для развития математических наук.

Сохранившиеся данные о Евклиде настолько малочисленны и сомнительны, что бытовала версия о присвоении псевдонима «Евклид» целым коллективам ученых из древней Александрии. Евклида Александрийского путают с греческим философом Евклидом из Мегар, учеником Сократа, жившим в 400 столетии до нашей эры. В средние века Евклида из Мегар даже считали автором «Начал».

Математика

Немалую часть свободного времени Евклид проводил в Александрийской библиотеке – храме знаний, основанном Птолемеем. В стенах этого учреждения древнегреческий ученый занялся объединением арифметических законов, геометрических принципов и теории иррациональных чисел в геометрию. Результаты своих трудов Евклид описал в книге «Начала» — сочинении, принесшем большой вклад в развитие математики.

Книга состоит из пятнадцати томов:

• В книге I автор рассказывает о свойствах параллелограммов и треугольников, завершая изложение применением теоремы Пифагора при расчете параметров прямоугольных треугольников.
• Книга под номером II описывает принципы и закономерности геометрической алгебры и восходит к багажу знаний, накопленных пифагорейцами.
• В книгах III и IV Евклид рассматривает геометрию окружностей, описанных и вписанных многоугольников. В ходе создания этих томов автор мог обратиться к использованию работ Гиппократа Хиосского.
• В V книге древнегреческий математик рассмотрел общую теорию пропорций, разработанную Евдоксом Книдским.
• В материалах VI книги автор прилагает общую теорию пропорций Евдокса Книдского к теории подобных фигур.
• Книги под номерами VII-IX описывают теорию чисел. При написании этих томов математик вновь обратился к материалам, созданным и собранным пифагорейцами – представителями учения, в котором центральную роль занимает число. В этих произведениях автор говорит о геометрических прогрессиях и пропорциях, доказывает бесконечность множества простых чисел, изучает четные совершенные числа, вводит понятие НОД (наибольшего общего делителя). Алгоритм нахождения такого делителя в настоящее время называется алгоритмом Евклида. Есть предположение, что VIII книгу написал не сам Евклид, а Архит Тарентский.

• Том под номером X – это наиболее сложный и объемный труд в составе «Начал», который содержит в себе классификацию иррациональностей. Авторство этой книги также доподлинно неизвестно: ее мог написать как сам Евклид, так и Теэтет Афинский.
• На страницах XI книги математик рассказывает об основах стереометрии.
• Книга XII содержит доказательства теорем об объемах конусов и пирамид, отношениях площадей кругов. Для построения этих доказательств используется метод исчерпывания. Большинство исследователей сходятся в том, что эту книгу также написал не Евклид. Вероятным автором является Евдокс Книдский.

• Материалы XIII книги содержат информацию о построении пяти правильных многогранников («платоновых тел»). Некоторую часть приведенных в томе построений мог разработать Теэтет Афинский.
• Книги XIV и XV, по общепризнанному мнению, также принадлежат другим авторам. Так, предпоследний том «Начал» написал Гипсикл (также живший в Александрии, но позже Евклида), а последний – Исидор Милетский (строивший храм святой Софии в Константинополе в начале шестого века до нашей эры).

До появления «Начал» Евклида труды с таким же названием, суть которых заключалась в последовательном изложении ключевых фактов теоретической арифметики и геометрии, были составлены Леонтом, Гиппократом Хиосским, Февдием. Все они практически исчезли из обихода после появления работы Евклида.

На протяжении двух тысяч лет пятнадцать томов «Начал» выступали в роли базового учебного пособия по геометрии. Работа переведена на арабский язык, затем – на английский. «Начала» перепечатывались сотни раз, и указанные в них базовых математических выкладок остаются актуальными по сей день.

Значительная часть материалов, которые автор включил в труд – не собственные открытия, а известные ранее теории. Суть работы Евклида заключалась в переработке материала, его систематизации и сведении разрозненных данных воедино. Некоторые книги Евклид начинал списком определений, в первой книге имеется также перечень аксиом и постулатов.

Постулаты Евклида делятся на две группы: общие понятия, включающие в себя общепризнанные научные утверждения, и геометрические аксиомы. Так, в первой группе встречаются такие утверждения:

«Если две величины порознь равны одной и той же третьей, то они равны между собой».

«Целое больше суммы частей».

Во второй группе находятся, например, следующие утверждения:

«От всякой точки до всякой точки можно провести прямую».

«Все прямые углы равны между собой».

«Начала» — не единственная книга, написанная Евклидом. Также он написал ряд работ по катоптрике (новой отрасли оптики, в немалой степени утверждавшей математическую функцию зеркал). Несколько работ ученый посвятил изучению конических сечений. Математик также разрабатывал предположения и гипотезы, касающиеся траектории движения тел и законов механики.

Он стал автором ключевых инструментов, которыми оперирует геометрия – так называемых «евклидовых построений». Многие работы этого древнегреческого мыслителя не дошли до наших дней.

Философия

В древние времена философия была тесно сплетена со многими другими отраслями научных знаний. Так, геометрия, астрономия, арифметика и музыка считались математическими науками, понимание которых необходимо для качественного изучения философии. Евклид развивал учение Платона о четырех элементах, которым приводятся в соответствие четыре правильных многогранника:

• стихию огня олицетворяет тетраэдр;
• воздушной стихии соответствует октаэдр;
• стихия земли ассоциируется с кубом;
• водная стихия связывается с икосаэдром.

В этом контексте «Начала» можно рассматривать как своеобразное учение о построении «платоновых тел», то есть пяти правильных многогранников. Учение содержит все необходимые предпосылки, доказательства и связки. Доказательство возможности построения таких тел завершается утверждением того факта, что никаких других правильных тел, за исключением данных пяти, не существует.

Практически каждая теорема Евклида в «Началах» соответствует также показателям учения о доказательстве Аристотеля. Так, автор последовательно выводит следствия из причин, формируя цепочку логических доказательств. При этом он доказывает даже утверждения общего характера, что также соответствует учению Аристотеля.

Личная жизнь

До нас дошла лишь некоторая информация о работе Евклида в науке, о его личной жизни же неизвестно практически ничего. Существует легенда, что царь Птолемей, решивший изучить геометрию, был раздосадован ее сложностью. Тогда он обратился к Евклиду и попросил его указать на более легкий путь к знаниям, на что мыслитель ответил: «К геометрии нет царской дороги». Выражение впоследствии стало крылатым.

Есть доказательства того, что при Александрийской библиотеке этот древнегреческий ученый основал частную математическую школу. В ней учились такие же энтузиасты науки, как и сам Евклид. Даже на закате своей жизни Евклид помогал ученикам в написании работ, создании собственных теорий и разработке соответствующих доказательств.

Точных данных о внешности ученого нет. Его портреты и скульптуры – это плод воображения их создателей, придуманный образ, передававшийся из поколения в поколение.

Смерть

Предположительно, Евклид скончался в 260-тых годах до нашей эры. Точные причины смерти не известны. Наследие ученого пережило его на две тысячи лет и вдохновляло многих великих людей спустя столетия после его кончины.

Существует мнение, что политический деятель Авраам Линкольн любил цитировать высказывания Евклида в своих речах и имел при себе несколько томов «Начал».

Ученые последующих лет базировали труды на работах Евклида. Так, русский математик Николай Лобачевский использовал материалы древнегреческого мыслителя для разработки гиперболической геометрии, или геометрии Лобачевского. Формат математики, который создал Евклид, ныне известен как «евклидова геометрия». Ученый также создал прибор для определения высоты тона струны и изучал интервальные соотношения, поспособствовав созданию клавишных музыкальных инструментов.

Библиография

• «Начала»
• «Данные»
• «О делении»
• «Явления»
• «Оптика»
• «Поризмы»
• «Конические сечения»
• «Поверхностные места»
• «Псевдария»
• «Катоптрика»
• «Деление канона»

Источник: 24smi.org

Евклид Биография, вклад и работа

Евклид Александрийский Он был греческим математиком, который заложил важные основы для математики и геометрии. Вклад Евклида в эти науки настолько важен, что до сегодняшнего дня они остаются в силе, после более чем 2000 лет после их формулирования.

Вот почему часто встречаются дисциплины, в названиях которых содержится прилагательное «евклидов», поскольку они основывают часть своих исследований на геометрии, описанной Евклидом..

• 1 Биография

• 1.1 Учебная работа
• 1.2 Личные характеристики
• 1.3 Смерть

• 3.1 Постулаты
• 3.2 Причины превосходства
• 3.3 Выпуски

• 4.1 Элементы
• 4.2. Теорема Евклида
• 4.3 Евклидова геометрия
• 4.4 Демонстрация и математика
• 4.5 Аксиоматические методы

биография

Точная дата рождения Евклида неизвестна. Исторические записи позволили определить его местонахождение где-то в 325 году до нашей эры..

По его образованию, по оценкам, имело место в Афинах, потому что работа Евклида показала, что он глубоко знал геометрию, которая была создана из школы Платона, разработанной в этом греческом городе.

Этот аргумент поддерживается до тех пор, пока не будет выведено, что Евклид, казалось, не знал работы афинского философа Аристотеля; по этой причине нельзя утверждать окончательно, что образование Евклида было в Афинах.

Преподавательская работа

В любом случае известно, что Евклид учил в Александрии, когда командовал королем Птолемеем I Сотером, который основал династию Птолемеев. Считается, что Евклид проживал в Александрии около 300 г. до н.э., и там он создал школу, посвященную преподаванию математики..

В этот период Евклид приобрел большую известность и признание благодаря своим способностям и навыкам учителя..

Анекдот, связанный с королем Птолемеем I, выглядит следующим образом: некоторые записи указывают, что этот король попросил Евклида научить его быстрому и краткому способу понимания математики, чтобы понимать и применять их.

Учитывая это, Евклид указал, что нет никаких реальных способов получить это знание. Намерение Евклида с этим двойным смыслом состояло также в том, чтобы показать царю, что, будучи не могущественным и привилегированным, может понимать математику и геометрию.

Личные характеристики

Вообще, Евклид изображался в истории как спокойный, очень добрый и скромный человек. Также сказано, что Евклид полностью понимал огромную ценность математики, и что он был убежден, что знание само по себе бесценно.

На самом деле, есть еще один анекдот об этом, который превзошел наше время благодаря доктору Хуану де Эстобео.

По-видимому, на уроке Евклида, в котором рассматривался предмет геометрии, студент спросил его, какую пользу он получит, получив эти знания. Евклид твердо ответил ему, объяснив, что знание само по себе является самым бесценным элементом, который существует.

Поскольку ученик, очевидно, не понимал и не подписывался на слова своего учителя, Евклид дал указание своему рабу дать ему несколько золотых монет, подчеркнув, что выгода от геометрии была гораздо более превосходной и глубокой, чем денежное вознаграждение..

Кроме того, математик указал, что нет необходимости получать прибыль от каждого знания, приобретенного в жизни; Сам факт получения знаний сам по себе является величайшим достижением. Это было видение Евклида в отношении математики и, в частности, геометрии.

смерть

Согласно записям в истории, Евклид умер в 265 году до нашей эры в Александрии, городе, в котором он прожил большую часть своей жизни..

завод

Элементы

Самым символическим произведением Евклида является Элементы, состоит из 13 томов, в которых он обсуждает такие разные темы, как геометрия пространства, неизмеримые величины, пропорции в общем поле, плоская геометрия и числовые свойства.

Это математический трактат широкого распространения, имевший большое значение в истории математики. Даже мысль о Евклиде преподавалась до восемнадцатого века, задолго до его времени, периода, в который возникли так называемые неевклидовы геометрии, противоречащие постулатам Евклида..

Первые шесть томов Элементы они занимаются так называемой элементарной геометрией, разрабатывают темы, связанные с пропорциями и методами геометрии, используемыми для решения квадратных и линейных уравнений.

Книги 7, 8, 9 и 10 посвящены исключительно решению численных задач, а последние три тома посвящены геометрии твердых элементов. В конце концов, в результате задумано регулярное структурирование пяти многогранников, а также их разграниченных сфер..

Само произведение представляет собой большой сборник концепций предыдущих ученых, организованный, структурированный и систематизированный таким образом, что позволил создать новые и трансцендентные знания.

постулаты

в Элементы Евклид предлагает 5 постулатов, а именно:

1- Наличие двух точек может привести к линии, которая.

2. Любой сегмент может непрерывно растягиваться по неограниченной прямой линии в одном и том же направлении..

3- Можно нарисовать центральную окружность в любой точке и на любом радиусе.

4- Совокупность прямых углов равна.

5- Если линия, которая пересекает два других, генерирует углы, меньшие, чем прямые на той же стороне, эти линии, растянутые до бесконечности, обрезаются в области, где находятся эти второстепенные углы..

Позднее пятый постулат был сделан по-другому: так как существует точка вне прямой, через нее можно провести только одну параллель..

Причины превосходства

Эта работа Евклида имела большое значение по разным причинам. Во-первых, отраженное там качество знаний сделало текст, используемый для преподавания математики и геометрии на базовых уровнях образования..

Как упоминалось ранее, эта книга продолжала использоваться в академической сфере до 18-го века; то есть, это было действительно в течение приблизительно 2000 лет.

Работа Элементы Это был первый текст, с помощью которого можно было войти в область геометрии; С помощью этого текста впервые можно сделать глубокие рассуждения, основанные на методах и теоремах..

Во-вторых, способ, которым Евклид организовал информацию в своей работе, также был очень ценным и превосходным. Структура состояла из заявления, к которому пришли как следствие существования нескольких принципов, ранее принятых. Эта модель была также принята в области этики и медицины.

издания

Что касается печатных изданий Элементы, первое произошло в 1482 году в Венеции, Италия. Работа была переведена на латынь с оригинального арабского.

После этого номера было опубликовано более 1000 изданий этой работы. Вот почему Элементы считается одним из самых читаемых книг в истории, наравне с Дон Кихот де ла Манча, Мигель де Сервантес Сааведра; или даже в то же время, что и сама Библия.

Основные вклады

элементы

Наиболее признанным вкладом Евклида была его работа под названием Элементы. В этой работе Евклид поднял важную часть математических и геометрических разработок, которые были сделаны в его время.

Теорема Евклида

Теорема Евклида демонстрирует свойства прямоугольного треугольника, рисуя линию, которая делит его на два новых прямоугольных треугольника, которые похожи друг на друга и, в свою очередь, похожи на исходный треугольник; то есть отношение пропорциональности.

Евклидова геометрия

Вклад Евклида произошел в основном в области геометрии. Разработанные им концепции доминировали в изучении геометрии в течение почти двух тысячелетий..

Трудно дать точное определение евклидовой геометрии. В общем, это относится к геометрии, которая охватывает все понятия классической геометрии, а не только разработки Евклида, хотя Евклид собрал и разработал несколько из этих концепций.

Некоторые авторы утверждают, что аспект, в котором Евклид внес больший вклад в геометрию, был его идеалом, основанным на неопровержимой логике.

Более того, учитывая ограниченность знаний своего времени, его геометрические подходы имели ряд недостатков, которые впоследствии усилили другие математики..

Демонстрация и математика

Евклид, наряду с Архимедом и Аполлином, считаются совершителями демонстрации как связанный аргумент, в котором делается вывод, оправдывая каждую ссылку.

Демонстрация является фундаментальной в математике. Считается, что Евклид разработал процессы математической демонстрации таким образом, который длится до сегодняшнего дня, и это важно в современной математике.

Аксиоматические методы

В презентации геометрии, сделанной Евклидом в Элементы считается, что Евклид сформулировал первую «аксиоматизацию» очень интуитивно и неформально.

Аксиомы — это определения и основные положения, которые не требуют доказательств. То, как Евклид представил аксиомы в своей работе, позже превратилось в аксиоматический метод..

В аксиоматическом методе предлагаются определения и суждения, так что каждый новый термин может быть исключен ранее введенными терминами, включая аксиомы, чтобы избежать бесконечной регрессии..

Евклид косвенно поднял вопрос о глобальной аксиоматической перспективе, которая способствовала развитию этой фундаментальной части современной математики..

ссылки

1. Бисон М. Брауэр и Евклид. Indagationes Mathematicae. 2017; 51: 1-51.
2. Корнелиус М. Евклид должен идти ? Математика в школе. 1973; 2(2): 16-17.
3. Флетчер В. К. Евклид. Математическая газета 1938: 22(248): 58-65.
4. Флориан С. Евклид Александрийский и бюст Евклида Мегарского. Наука, Новая серия. 1921; 53(1374): 414-415.
5. Эрнандес Й. Более двадцати веков геометрии. Журнал Книги. 1997;10(10): 28-29.
6. Медер А. Е. Что не так с Евклидом?? Учитель математики. 1958; 24(1): 77-83.
7. Тейсен Б. Ю. Евклид, Относительность и парусный спорт. История Mathematica. 1984; 11: 81-85.
8. Валле Б. Полный анализ бинарного евклидова алгоритма. Международный симпозиум по алгоритмической теории чисел. 1998; 77-99.

Источник: ru.thpanorama.com