1. 2 прямые делят плоскость на 4 части если они пересекаются ; или на 3 части, если прямые параллельны.
2. 3 прямые делят плоскость на 6 частей, если пересекаются в одной точке или две из них параллельны, а третья их пересекает ; если попарное пересечение и при этом никакие две не параллельны, то на 7 частей ; и на 4 части, при условии, что все эти прямые параллельны.
3. 4 прямые делят плоскость на 8 частей. если одна прямая пересекает три параллельных, если же две пары параллельных пересекаются в 4 точках, то плоскость делится на 9 частей, то же получим, если две параллельны, а две другие пересекаются в точке, принадлежащей одной из параллельных прямых; если все 4 прямые параллельны, то они делят плоскость на 5 частей, если две параллельные, а две другие пересекаются в точке, не принадлежащей ни одной из параллельных, то
они делят плоскость на 10 частей, если две пересекаются, две другие тоже пересекаются, и никакие не параллельны между собой, и точки пересечения двух пересекающихся пар не совпадают. то получим 11 частей плоскости.
Итак, 4 прямые делят плоскость на 5;8;9;10;11 частей.
Источник: megashkola.com
Ответьте пж Рассмотри и определи все возможные случаи, на сколько частей плоскость делят в ней …
Ответьте пж
Рассмотри и определи все возможные случаи, на сколько частей плоскость делят в ней расположенные прямые.
(как ответ введи число возможных частей, через запятую, но без пробелов)
1. 2 прямые делят плоскость на
части;
2. 3 прямые делят плоскость на
частей;
3. 4 прямые делят плоскость на
частей.
Пояснение: считаем, что отдельная часть плоскости такая, что в другую часть можно попасть только переходя через границу — прямую.
София Криушечева Вопрос задан 22 сентября 2019 в 5 — 9 классы, true»> Поделиться
Плоскость. Пересекающиеся прямые. 6 класс.
Источник: matfaq.ru
На сколько частей прямая делит плоскость чертеж

Давайте посмотрим на поверхности стола или тетрадного листа, мы можем о них сказать, что они плоские, но плоскостью их назвать нельзя, потому что эти поверхности являются лишь частью плоскости, так как имеют края. А плоскость не имеет края, она безгранична и простирается во всех направлениях.
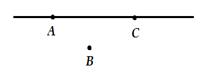
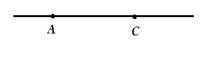
Построим отрезок АС и продолжим его в обе стороны за точки А и С по линейке. Получим прямую. Прямая не имеет концов, она бесконечна. Прямую обозначают двумя заглавными латинскими буквами (на рисунке вы видите прямую АС или СА) или одной маленькой латинской буквой (например, прямая а). Точки А и С лежат на этой прямой.
Математика 5 класс (Урок№21 — Прямая, луч, отрезок.)
Говорят, точки А и С принадлежат прямой АС.
Отметим точку В, не лежащую на прямой АС. Говорят, точка В не принадлежит прямой АС.
Если провести прямую на плоскости, то она разделит плоскость на две части – на две полуплоскости.
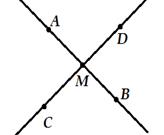
Если две прямые имеют одну общую точку, то говорят, что они пересекаются в этой точке. На рисунке прямые АВ и СD пересекаются в точке М.
Через две точки плоскости можно провести только одну прямую! Через одну точку можно провести бесконечно много прямых.

Перейдем к следующему понятию – луч. Если на прямой отметить точку, то она разделит прямую на две части, каждую из которых называют лучом. Луч имеет начало, но не имеет конца. В отличие от прямой луч бесконечен только в одну сторону. Чтобы обозначить луч, надо назвать его начало заглавной латинской буквой и какую-нибудь точку на луче. Например, луч ВС.
Начало луча в точке В, именно она пишется на первом месте.
§ 4 Практические задания
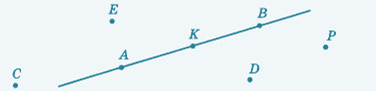
Давайте выполним несколько заданий по данному рисунку.
1) нужно назвать все прямые, которые изображены на данном чертеже.
2) какие точки не принадлежат прямой АК?
3) пересекаются ли прямая АВ и луч СD?
4) пересекаются ли прямая АВ и луч СЕ?
1) прямая АВ или ВА, АК или КА, ВК или КВ
2) точки С, Е, D, Р
3) да. Так как луч СD берет начало в точке С и продолжается за точку D, тем самым пересекая прямую АК
При ответе на все эти вопросы, пересекаются ли прямые, отрезки и лучи, надо помнить: что прямая бесконечна, отрезок ограничен двумя концами, а луч имеет начало, но не имеет конца.
Список использованной литературы:
- Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. — М: 2013.
- Дидактические материалы по математике 5 класс. Автор — Попов М.А. — 2013 год
- Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор — Минаева С.С. — 2014 год
- Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. — 2010 год
- Контрольные и самостоятельные работы по математике 5 класс. Авторы — Попов М.А. — 2012 год
- Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009. — 270 с.: ил.
Источник: znaika.ru
