Сколько осей симметрии имеет отрезок прямая луч

Симметричность точек относительно прямойСимметричность фигуры относительно прямойСимметричность точек относительно точкиСимметричность фигуры относительно точкиСимметрия на координатной плоскостиСимметрия вокруг насМатематики о симметрииПроверим знанияЗаданияСодержание

• Главная
• Геометрия
• Презентация по геометрии на тему; Осевая и центральная симметрия

Слайд 1Центральная
и осевая
симметрия

Слайд 2Симметричность точек относительно прямой
Симметричность фигуры относительно прямой
Симметричность точек относительно точки
Симметричность фигуры

относительно точки
Симметрия на координатной плоскости
Симметрия вокруг нас
Математики о симметрии
Проверим знания
Задания

№417. Сколько осей симметрии имеет: а) отрезок; б) прямая; в) луч?

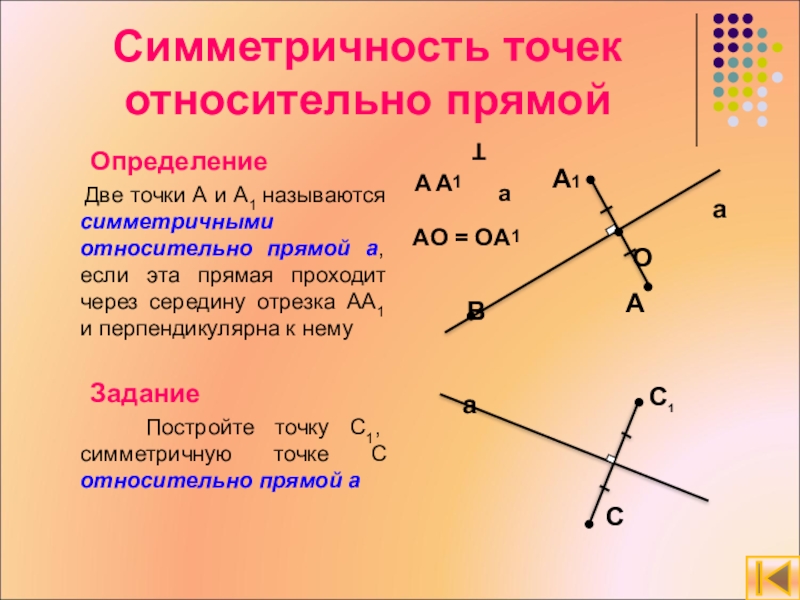
Слайд 3Симметричность точек относительно прямой
Определение
Две точки А и А1

называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему

Задание
Постройте точку C1, симметричную точке C относительно прямой а

Слайд 4Симметричность фигуры относительно прямой
Определение
Фигура называется симметричной относительно прямой, если

для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре

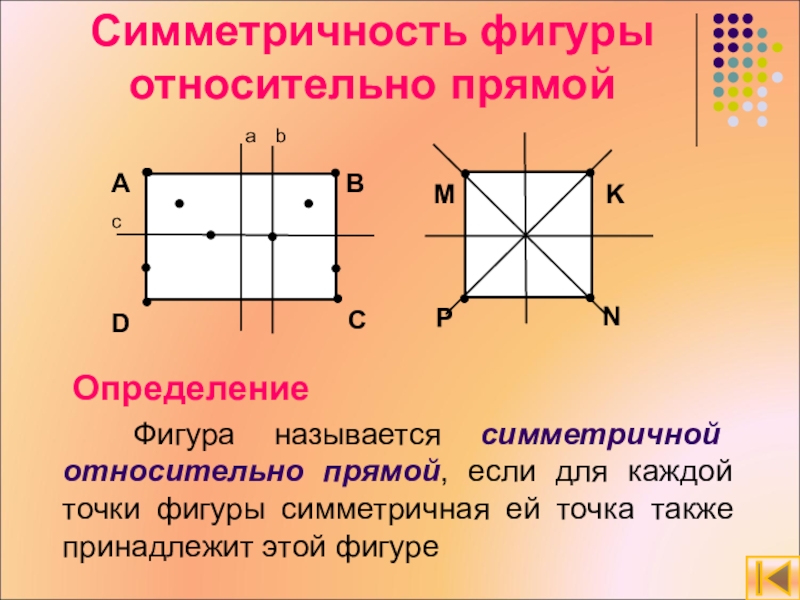
Слайд 5Какие из данных фигур имеют ось симметрии? Сколько?

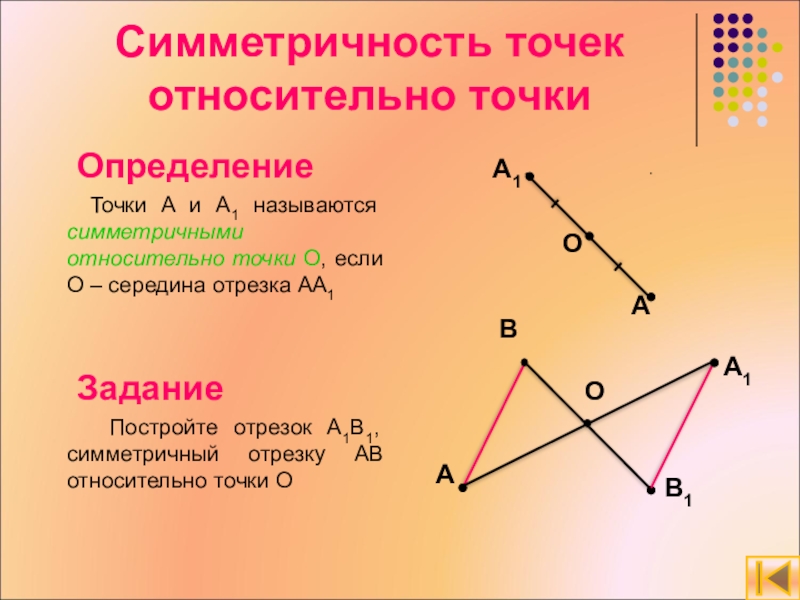
Слайд 6Симметричность точек относительно точки
Определение
Точки A и A1 называются симметричными

относительно точки О, если О – середина отрезка AA1

Задание
Постройте отрезок A1B1, симметричный отрезку AB относительно точки О

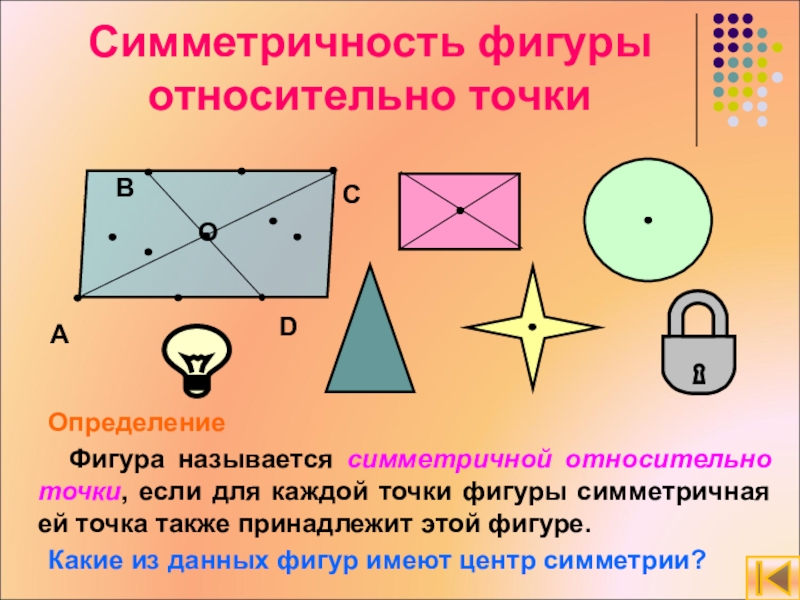
Слайд 7Симметричность фигуры относительно точки
Определение
Фигура называется симметричной относительно точки,

если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.
Какие из данных фигур имеют центр симметрии?

Слайд 8

Симметричность на координатной плоскости

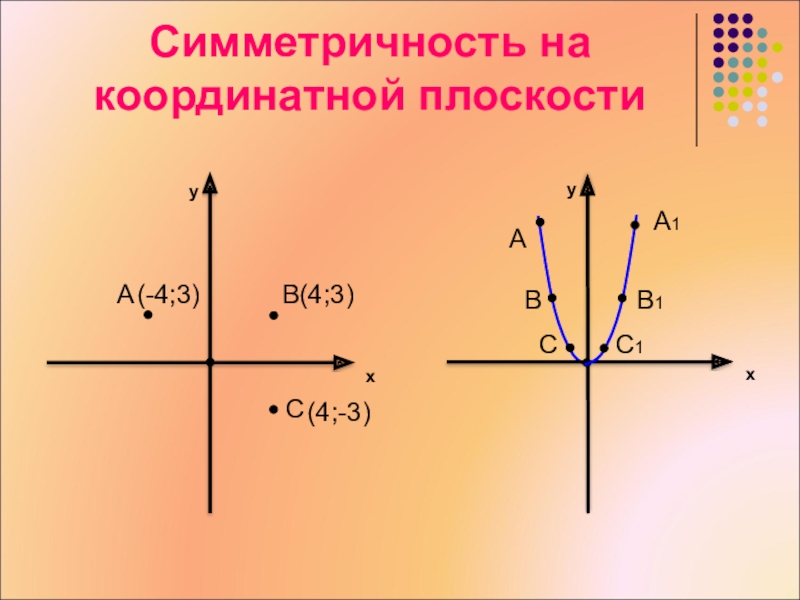
Слайд 9

Симметричность на координатной плоскости
y
y
x
x
A

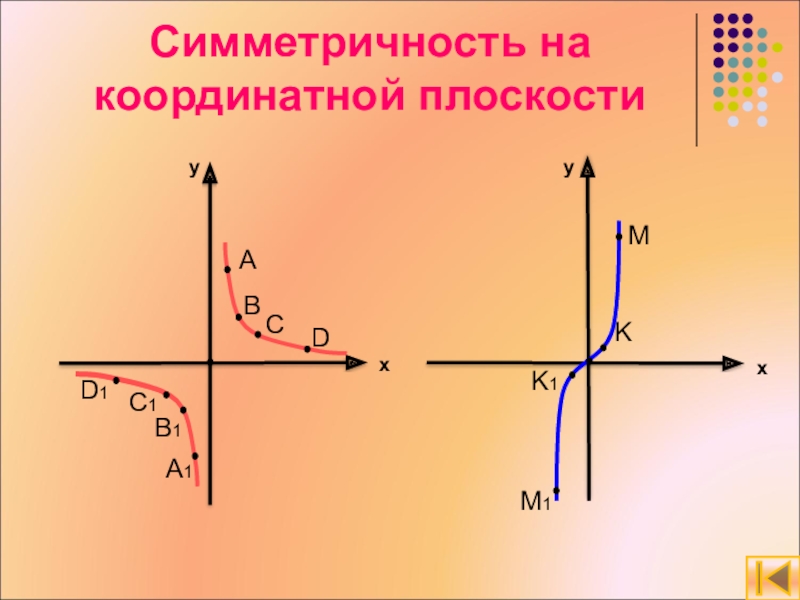
Слайд 10Симметрия в природе

Слайд 11Симметрия в архитектуре

Слайд 12Симметрия в искусстве

Слайд 13Математики о симметрии
Математик любит прежде всего симметрию

Красота тесно связана с симметрией
Вейль Г.

Симметрия … является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство
Вейль Г.

Для человеческого разума симметрия обладает, по — видимому, совершенно особой притягательной силой
Фейнман Р.

Источник: shareslide.ru

Презентация «Преобразования на плоскости» (7 класс) по математике – проект, доклад

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

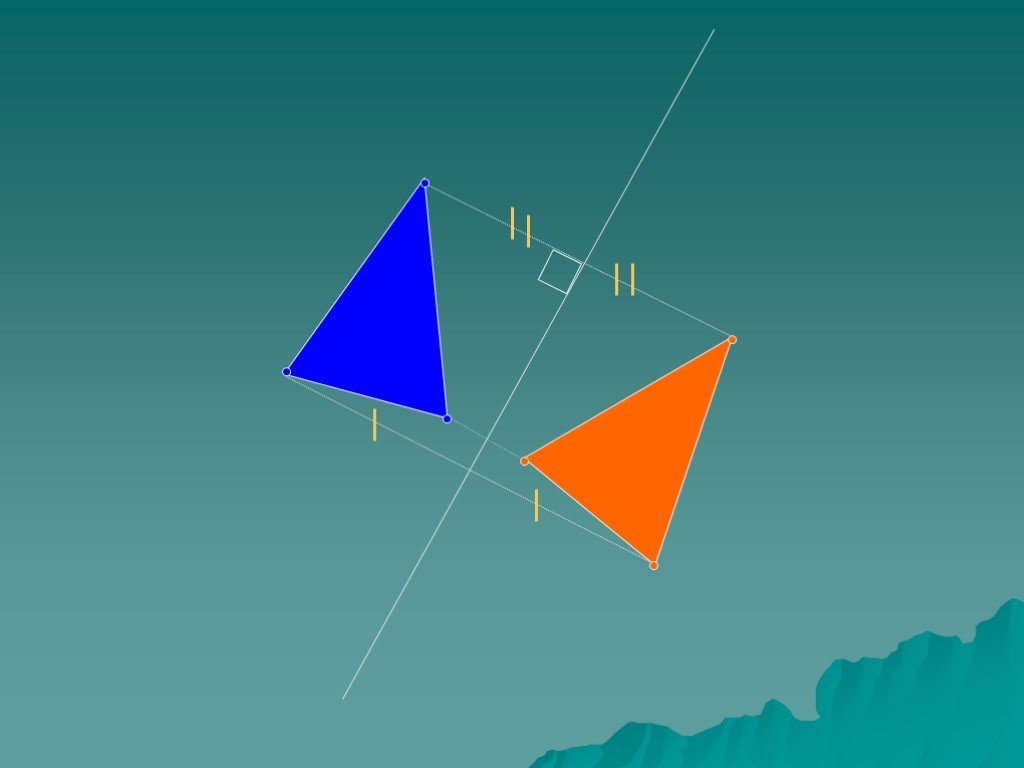
Слайд 6

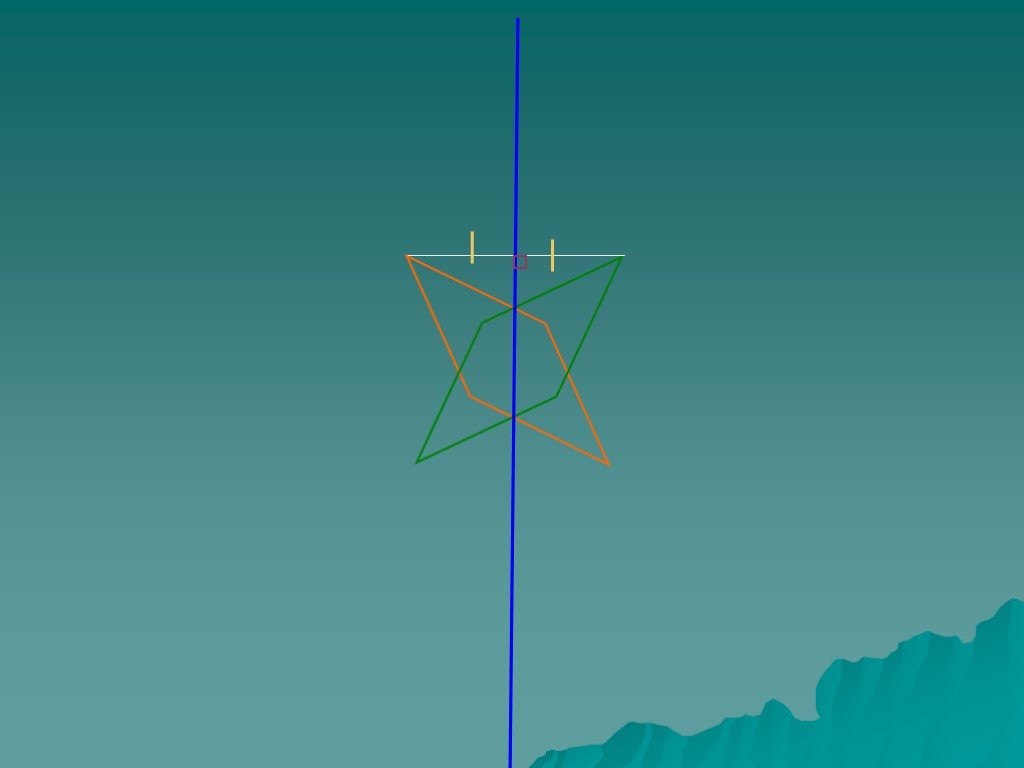
Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15

Слайд 16

Слайд 17

Слайд 18

Слайд 19

Слайд 20

Слайд 21

Слайд 22

Слайд 23

Слайд 24

Слайд 25

Слайд 26

Слайд 27

Слайд 28

Слайд 29

Слайд 30

Слайд 31

Слайд 32

Слайд 33

Слайд 34

Слайд 35

Слайд 36

Слайд 37

Презентацию на тему «Преобразования на плоскости» (7 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад — нажмите на соответствующий текст под плеером. Презентация содержит 37 слайд(ов).

Слайды презентации

Преобразования на плоскости

МОУ СОШ № 5 г. Ивантеевка учитель математики Любецкая Н. Ф.

О симметрия! Гимн тебе пою! Тебя повсюду в мире узнаю. Ты в Эйфелевой башне, в малой мошке, Ты в елочке, что у лесной дорожки. С тобою в дружбе и тюльпан, и роза, И снежный рой – творение мороза!

Симметрия (греч.) — соразмерность, пропорциональность, одинаковость в расположении частей.

Симметрия относительно прямой Симметрия относительно точки Поворот Симметрия в природе Симметрия в архитектуре

Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему

а – ось симметрии

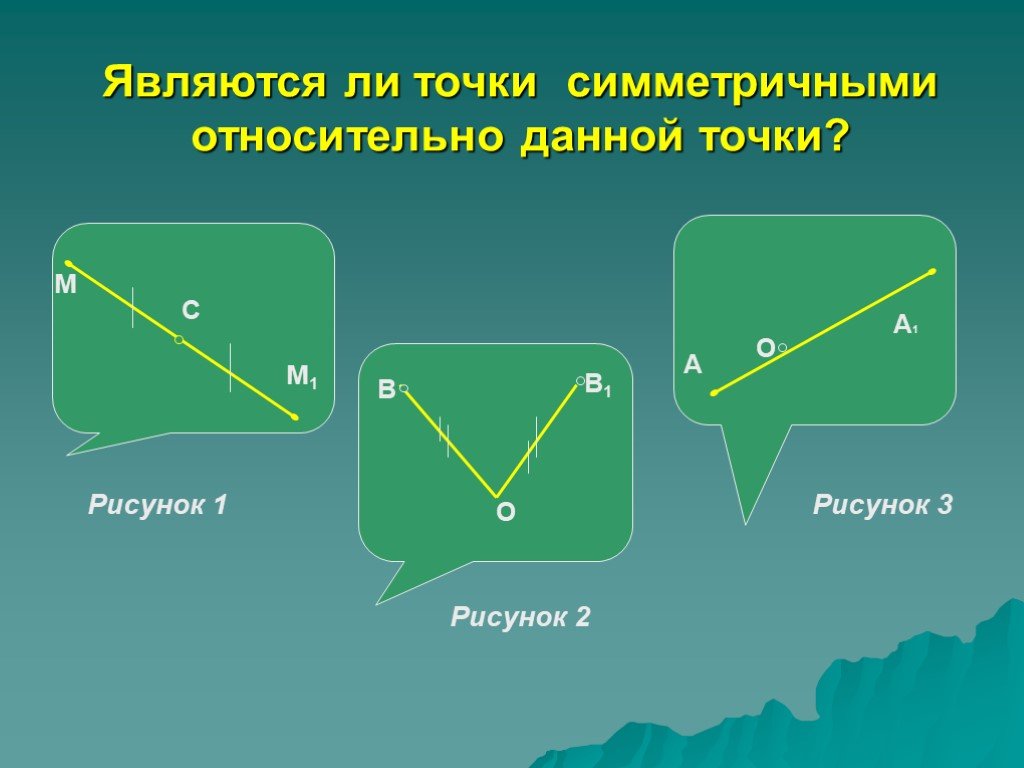
Являются ли данные точки симметричными ?

М М1 m С D b B В1 а Рисунок 1 Рисунок 2 Рисунок 3

Сколько осей симметрии имеет: Отрезок Прямая Луч

А В О Е одна множество Ни одной Задачи:

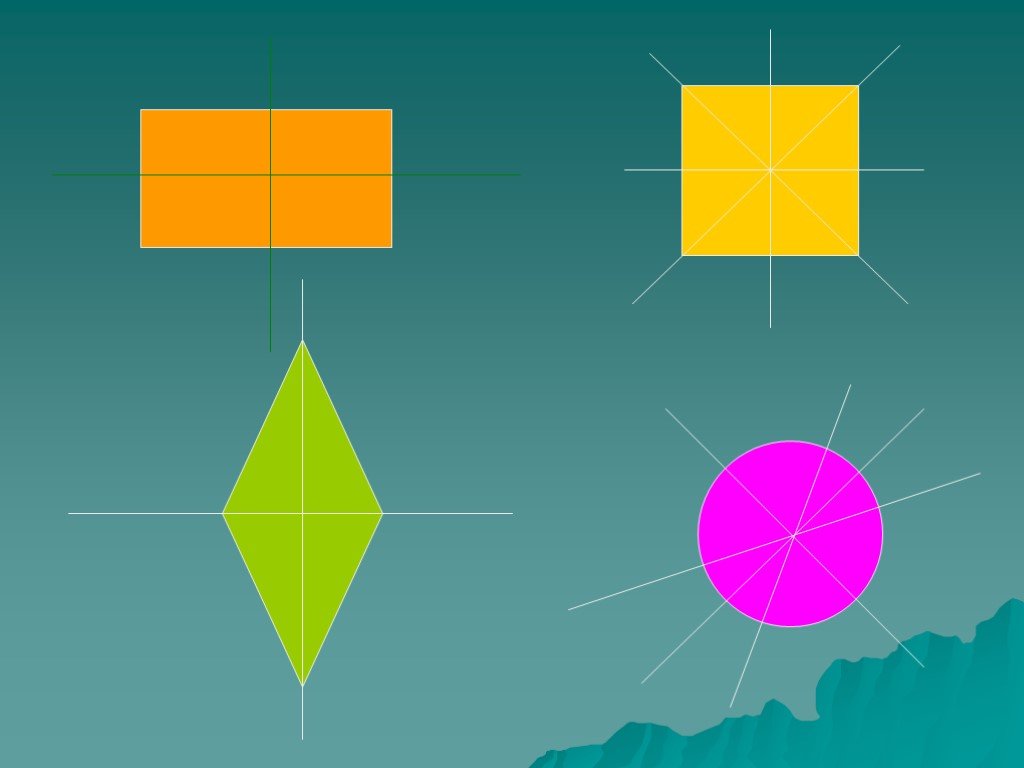
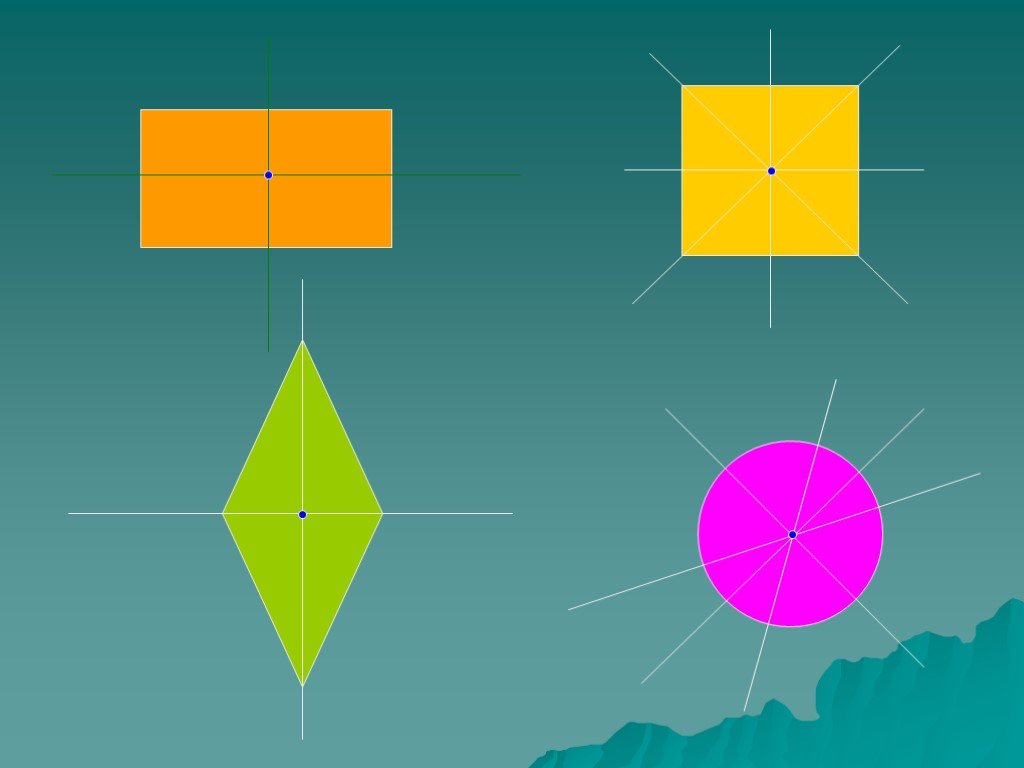
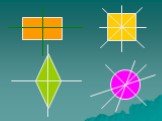
Какие из этих фигур имеют ось симметрии?

Сколько осей симметрии имеет каждая фигура?

5 6 3 1 2 4 Бесконечно много

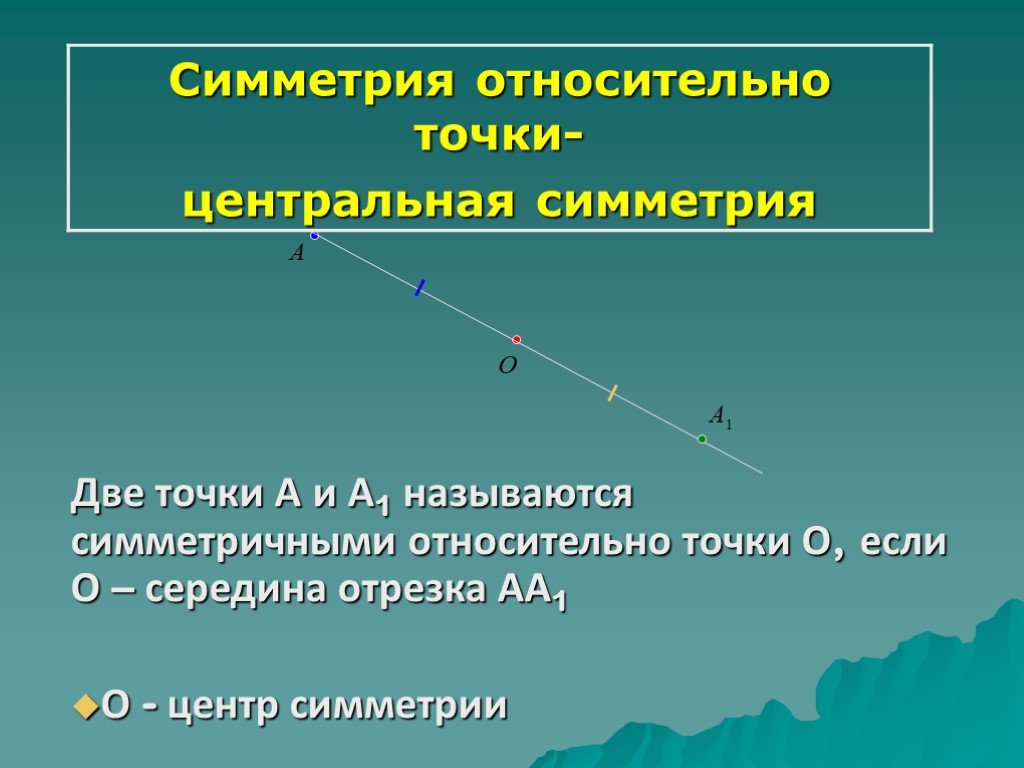
Две точки А и А1 называются симметричными относительно точки О, если О – середина отрезка АА1 О — центр симметрии

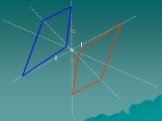
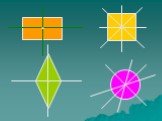
Являются ли точки симметричными относительно данной точки?

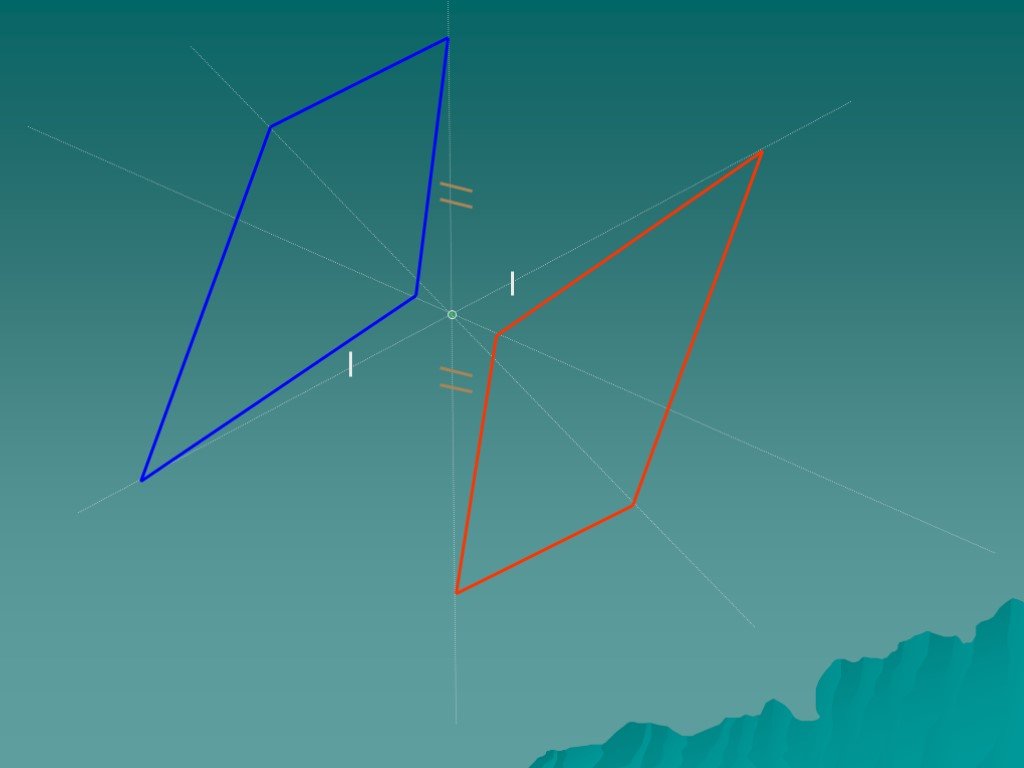
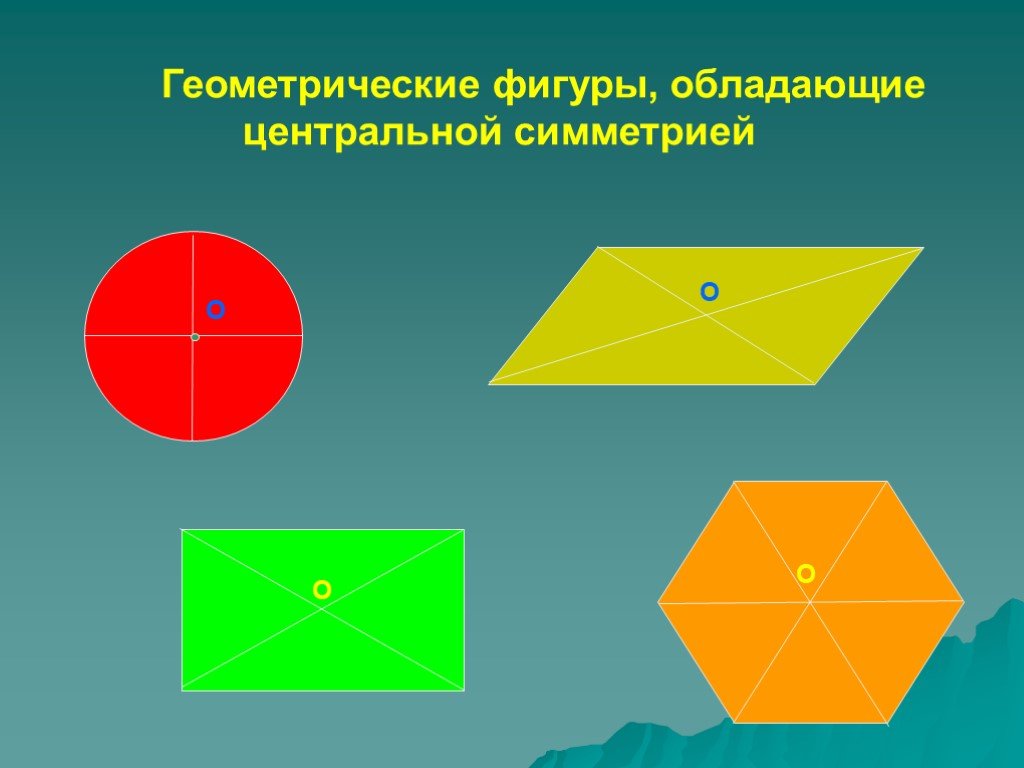
Геометрические фигуры, обладающие центральной симметрией

Имеют ли центр симметрии: Отрезок Прямая Луч

Задачи один Ни одного О1 О2

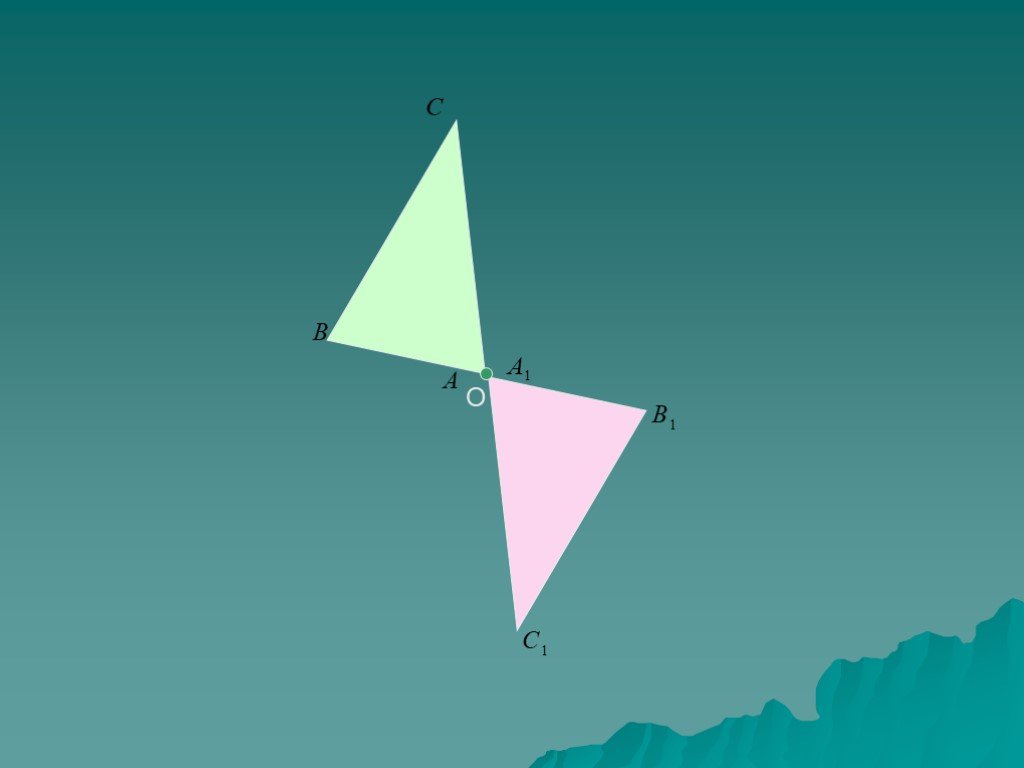
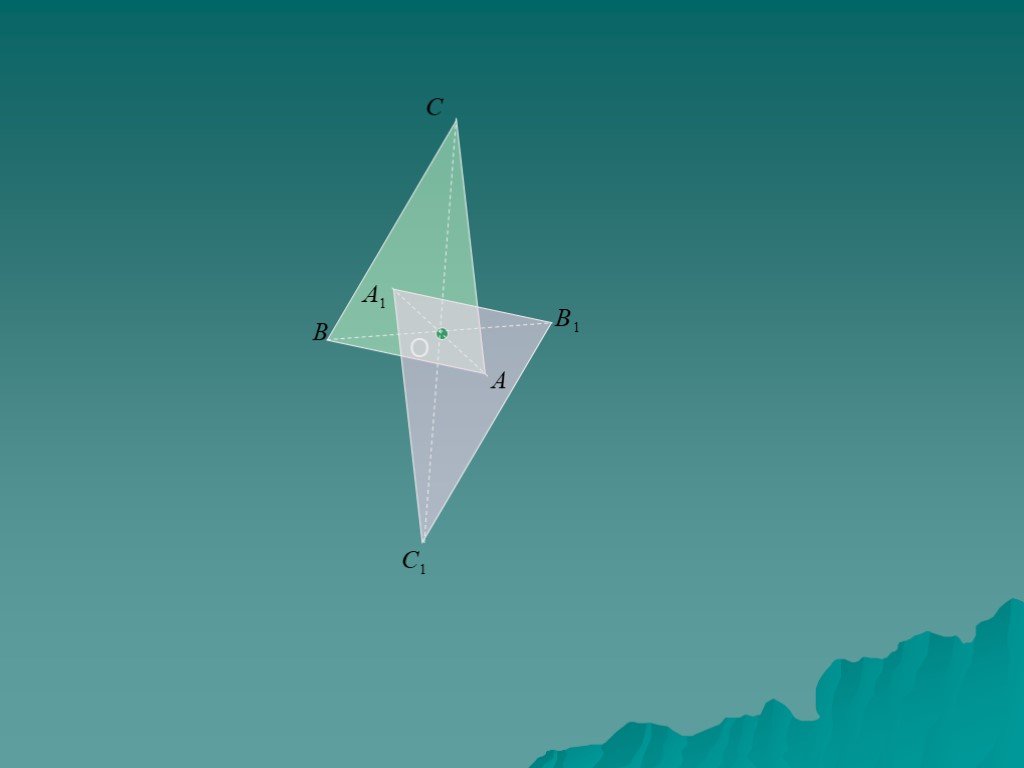
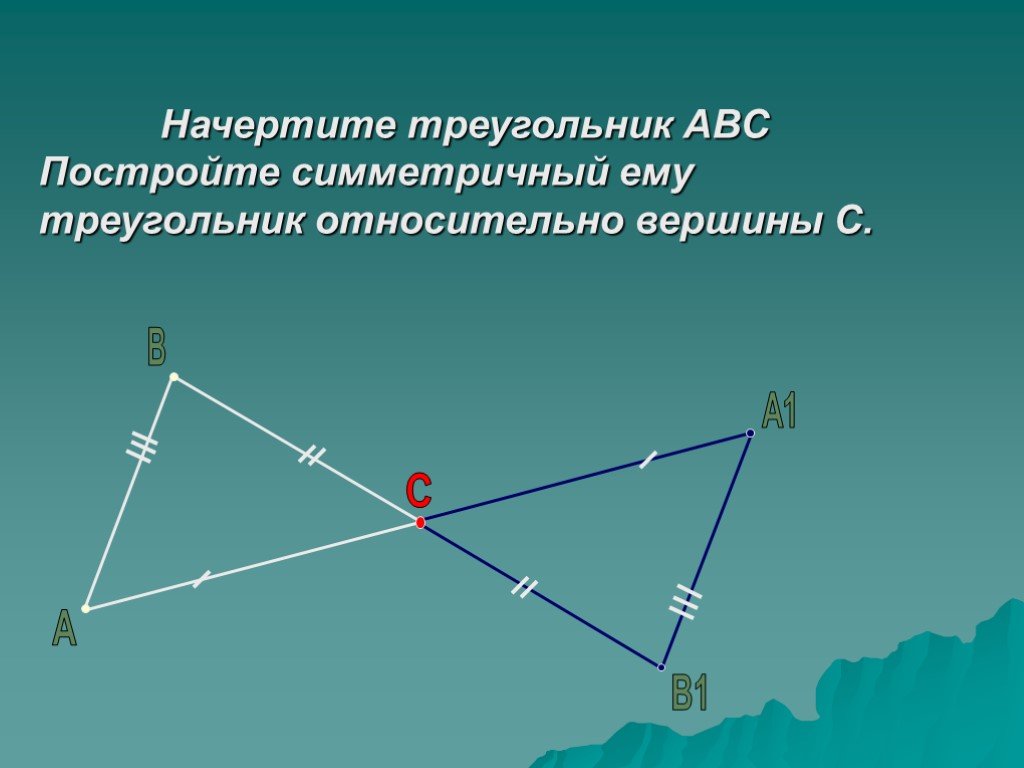
Начертите треугольник АВС Постройте симметричный ему треугольник относительно вершины С.

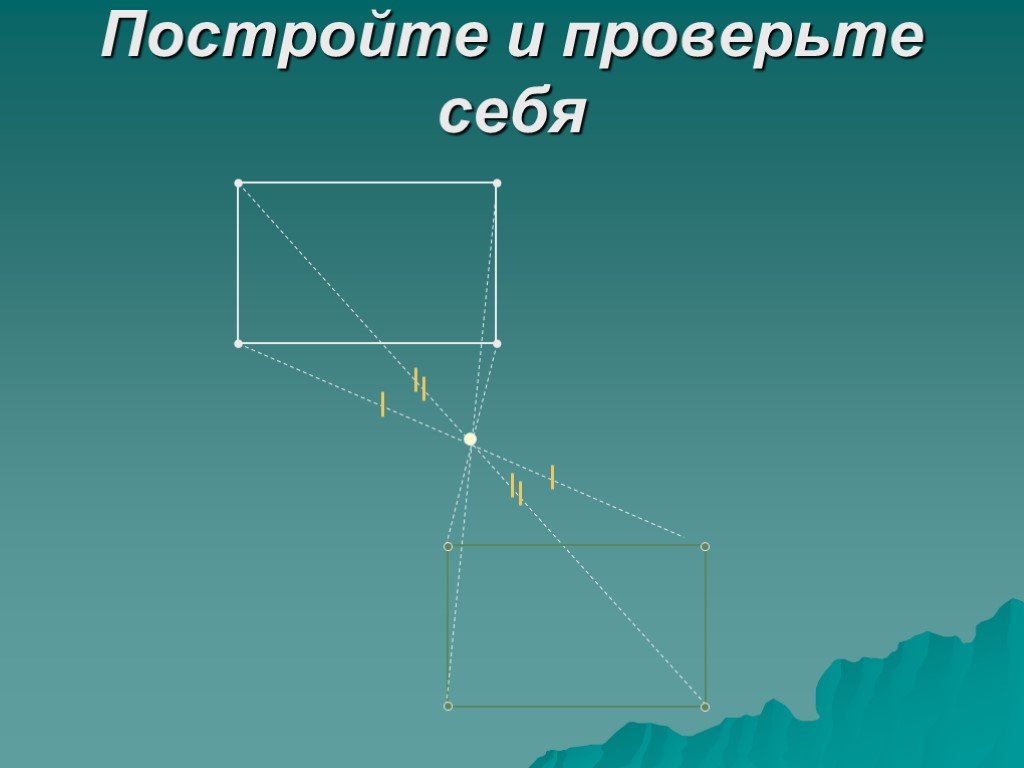
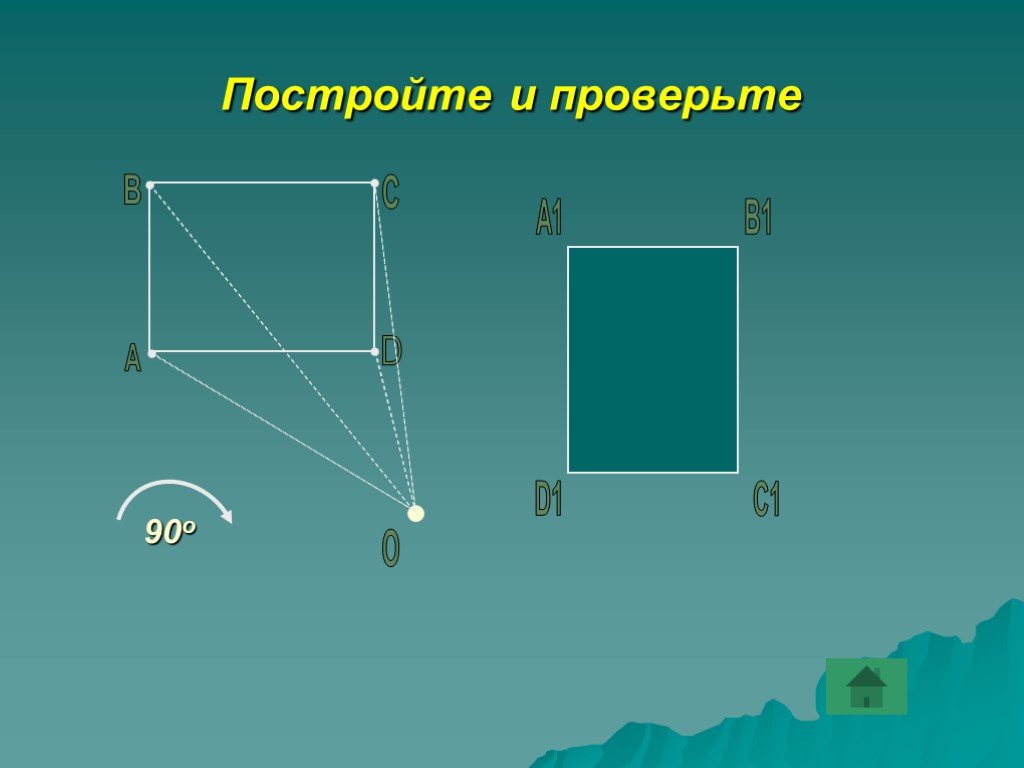
Постройте и проверьте себя

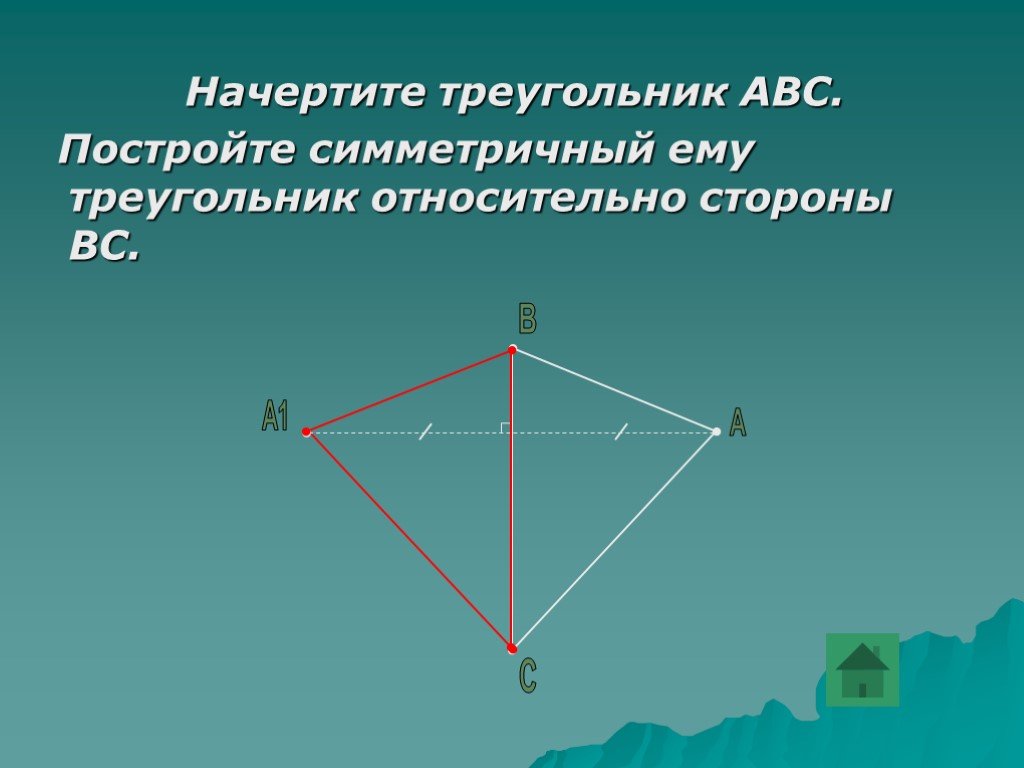
Начертите треугольник АВС. Постройте симметричный ему треугольник относительно стороны ВС.

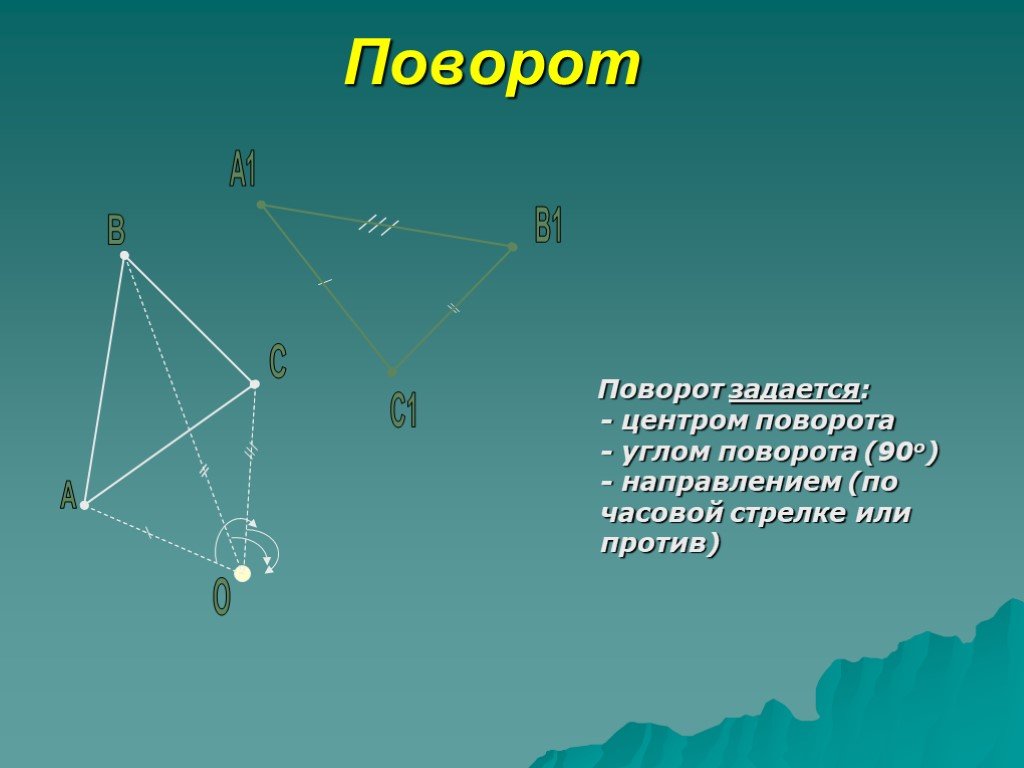
Поворот задается: — центром поворота — углом поворота (90о) — направлением (по часовой стрелке или против)

Постройте и проверьте

Симметрия в балете

Знаменитые фуэте, когда балерина вращается на одной ножке 6 раз, 12, …, 32 раза! Их повторяемость рождает эстетический эффект, служащий достойным завершением танца!

Листья располагаются на стволе по винтовой линии, чтобы заслонять друг от друга солнечный свет.

Антисимметрия – это противоположность симметрии, ее отсутствие.

Диссимметрия – это частичное отсутствие симметрии, её расстройство, выраженное в наличии одних симметричных свойств и отсутствии других.

С какими новыми понятиями познакомились? Что нового узнали о геометрических фигурах? Приведите примеры геометрических фигур, обладающих осевой симметрией. Приведите пример фигур, обладающих центральной симметрией. Приведите примеры предметов из окружающей жизни, обладающих одной или двумя видами симметрии.

Источник: prezentacii.org

wiki.eduVdom.com

Записаться
на занятия (831) 247 47 55
eduVdom.com

Геометрия:

Контакты

eduVdom.com
+7 910 874 73 73
+7 904 064 04 04
Больше контактов.
Оставить отзыв.
subjects:geometry:центральная_и_осевая_симметрии
Четырехугольники
Центральная и осевая симметрии

Центральная и осевая симметрии

Центральная симметрия

Две точки А и А1 называются симметричными относительно точки О, если О — середина отрезка АА1 (рис.1). Точка О считается симметричной самой себе.

Пример центральной симметрии

Точки А и А1 – симметричные относительно точки О

Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.

Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм (рис.2).

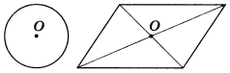
Фигуры, обладающие центральной симметрией

Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма — точка пересечения его диагоналей. Прямая также обладает центральной симметрией, однако в отличие от окружности и параллелограмма, которые имеют только один центр симметрии (точка О на рис.2), у прямой их бесконечно много — любая точка прямой является ее центром симметрии.

Осевая симметрия

Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему (рис.3). Каждая точка прямой а считается симметричной самой себе.

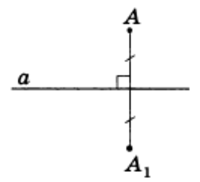
Точки А и А1 — симметричные относительно прямой а

Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры.

Примеры таких фигур и их оси симметрии изображены на рисунке 4.

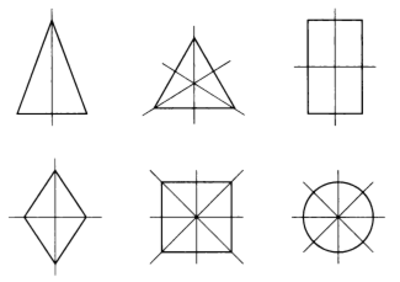
Заметим, что у окружности любая прямая, проходящая через ее центр, является осью симметрии.

Сравнение симметрий

Центральная и осевая симметрии

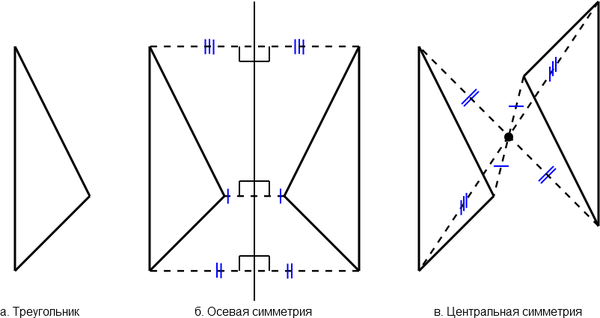
Построение треугольника (а) симметрично относительно оси (б) и точки (в)

Пример

Сколько всего осей симметрии имеет фигура, изображённая на рисунке?

Дополнительно

Геометрия ( Справочник )

Рекомендуем для обучения:

YouTube

← Трапеция	Пропорциональные отрезки →
Оси симметрии на YouTube
Подобие произвольных фигур

subjects/geometry/центральная_и_осевая_симметрии.txt · Последние изменения: 2022/04/01 20:09 — ¶

Инструменты страницы

• Показать исходный текст
• История страницы
• Ссылки сюда
• Свернуть / развернуть всё
• Наверх

Записаться на занятия

Записаться на занятия к репетитору

• +7 (910) 874 73 73
• +7 (905) 194 91 19
• +7 (831) 247 47 55

Источник: www.wiki.eduvdom.com