После того как вы поделитесь материалом внизу появится ссылка для скачивания.
Получить код —>
Подписи к слайдам:
- Симметрия
- относительно прямой
- Л.С. Атанасян «Геометрия 7-9»
- Симметрия относительно прямой
- А
- А1
- a
- Точки А и А1 называются симметричными относительно прямой (ось симметрии), если прямая проходит через середину отрезка АА1 и перпендикулярна к этому отрезку. Каждая точка прямой считается симметричной самой себе.
- a
- a
- a
- Симметрия относительно прямой называется осевой симметрией
- А
- Построить отрезок А1В1 симметричный отрезку АВ относительно прямой
- В
- a
- А1
- В1
- a
- Прямая – ось симметрии
- a
- Построить отрезок А1В1 симметричный отрезку АВ относительно прямой
- В
- a
- А
- a
- А1
- В1
- Прямая – ось симметрии
- a
- Построить треугольник А1В1С1 симметричный треугольнику АВС относительно прямой
- a
- Прямая – ось симметрии
- a
- А
- С
- В
- А1
- С1
- В1
- a
- Построить треугольник А1В1С1 симметричный треугольнику АВС относительно прямой
- a
- Прямая – ось симметрии
- a
- А
- В
- a
- А1
- С
- В1
- Построить треугольник А1В1С1 симметричный треугольнику АВС относительно прямой
- a
- Прямая – ось симметрии
- a
- А
- В
- a
- В1
- С
- Прямая – ось симметрии
- a
- А
- В
- a
- А1
- В1
- С
- С1
- Булавин Павел, 9В класс.
- Прямая m – ось симметрии
- m
- C
- C1
- B
- B1
- a
- A
- A1
- Савченко Миша, 9В класс.
- Прямая а – ось симметрии
- l
- A
- A1
- B
- B1
- C
- C1
- Если фигура имеет ось симметрии, то говорят, что она обладает осевой симметрией. Фигура может иметь одну или несколько осей симметрии.
- Фигура называется симметричной относительно оси , если для каждой точки фигуры симметричная ей точка относительно прямой также принадлежит этой фигуре.
- a
- a
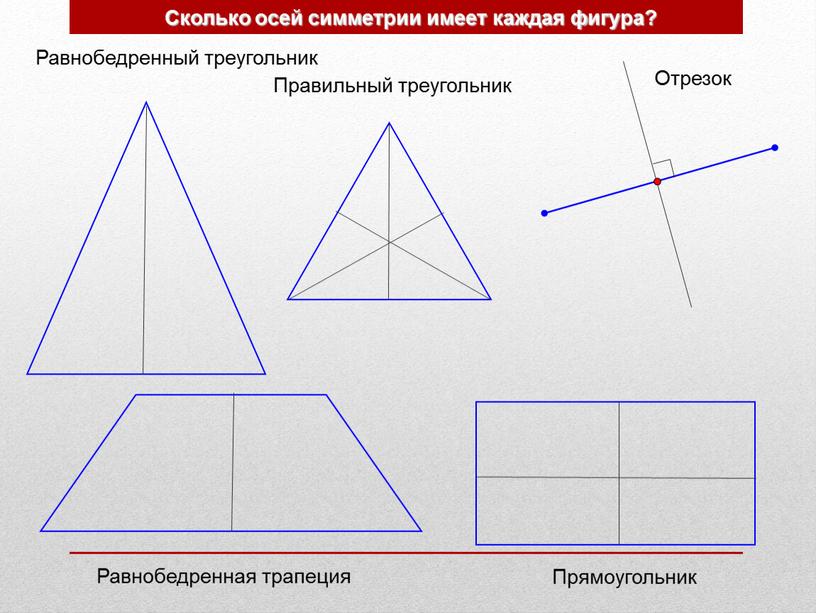
- Правильный треугольник
- Равнобедренный треугольник
- Отрезок
- Прямоугольник
- Сколько осей симметрии имеет каждая фигура?
- Равнобедренная трапеция
- прямая
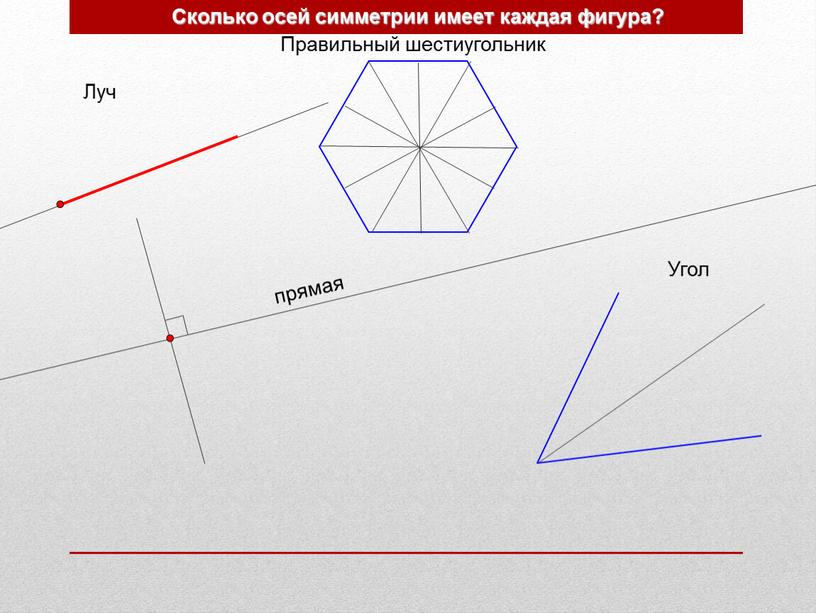
- Луч
- Правильный шестиугольник
- Параллелограмм
- Угол
- Сколько осей симметрии имеет каждая фигура?
- Какие буквы имеют ось симметрии?
- А
- Б
- Г
- Ж
- Э
- Ю
- Н
- Ш
- 0
- П
- Ф
- W
- U
- D
- R
- Y
- S
- V
- Какие буквы имеют ось симметрии?
- Х
- С
- М
- В
- Симметрия в природе
- http://2krota.ru/2009/06/27/babochki-chast-2.html
- http://2krota.ru/uploads/posts/2009-06/1245402488_822717426.jpg
- Симметрия в природе
- http://pda.privet.ru/post/69351242
- http://s56.radikal.ru/i152/0910/10/4879b89c5180.jpg
- Симметрия в природе
- http://www.potolok-spb.ru/art/images/butterfly/butterfly14.jpg
- Симметрия в танцевальной постановке необходима, однако для произведения должного эффекта она должна сопровождаться асимметрией
- http://www.idance.ru/articles/20/767p_sy4.jpg
- Символ вечной любви, Индии, симметрии, торжества персидской архитектуры — мавзолей Тадж-Махал
- http://www.indostan.ru/indiya/foto-video/2774/3844_9_o.jpg
- Узнаете этих женщин? Это очень известный человек в нашей стране. На одной картинке совмещены левые половинки фотографии-оригинала, на другой – правые. Кто же изображен на фотографии оригинале?
- На самом деле лицо человека не является идеально симметричным.
- О
- Р
- И
- Г
- И
- Н
- А
- Л
- http://viperson.ru/data/200708/Al1.jpg
- Рассмотрим другую
- фотографию.
- http://afisha.yandex.ru/media/events/images/6a00a930da073a0a935bea14964e33b2.jpg
- http://ru.trinixy.ru/pics2/20070323/podb/5/pugacheva_12.jpg
- 1 2 3 4 5 6 7 х
- -7 -6 -5 -4 -3 -2 -1
- 7
- 6
- 5
- 4
- 3
- 2
- 1
- -1
- -2
- -3
- -4
- -5
- -6
- -7
- у
- Симметрия на координатной плоскости
- Центральная симметрия
- 1 2 3 4 5 6 7 х
- -7 -6 -5 -4 -3 -2 -1
- 7
- 6
- 5
- 4
- 3
- 2
- 1
- -1
- -2
- -3
- -4
- -5
- -6
- -7
- у
- Осевая симметрия
- Симметрия на координатной плоскости
Источник: uchitelya.com
Сколько осей симметрии имеет каждая фигура пентамино ➄ На уроках геометрии
№417. Сколько осей симметрии имеет: а) отрезок; б) прямая; в) луч?
Симметричные фигуры
Фигуры могут обладать симметрией относительно точки и относительно прямой.
Фигура симметрична относительно точки тогда, когда в ней есть некая точка (центр симметрии), относительно которой у каждой другой точки фигуры есть симметричная точка этой же фигуры. Например, если отрезок разделить пополам, то центральная его точка будет центром симметрии, а концы отрезков симметричными относительно его. То есть симметричные точки находятся на одинаковом расстоянии от центра симметрии.
Еще одним примером фигуры, обладающей центральной симметрией является круг. Если представить, что в центр круга вбит гвоздик, то как круг не поворачивай, он всегда совместится сам с собой.
Параллелограмм также обладает центральной симметрией. Центром симметрии у него является точка пересечения диагоналей. Если параллелограмм повернуть на 180°, то он совместится сам с собой.
Все правильные многоугольники с четным количеством сторон (2n) также обладают центральной симметрией. Точками симметрии являются центры таких многоугольников.
Также многие фигуры симметричны относительно прямой. В таких фигурах можно провести прямую (ось симметрии), относительно которой все другие точки фигуры будут иметь соответствующие симметричные им точки. То есть если такую фигуру перегнуть вдоль оси симметрии, то половинки полностью совместятся. Другими словами, такие фигуры обладают осевой симметрией.
Угол (кроме развернутого) имеет одну осевую симметрию. Ось симметрии проходит по биссектрисе угла. А вот развернутый угол по сути представляет собой прямую, поэтому обладает центральной симметрией (симметрией относительно точки).
У равнобедренного треугольника есть одна ось симметрии. Это медиана (она же биссектриса и высота) к основанию. А вот у равностороннего треугольника три оси симметрии. Точка пересечения биссектрис равностороннего треугольника — является точкой симметрии фигуры. Таким образом, равносторонний треугольник обладает и центральной и осевой симметрией.
Равнобедренный — только осевой.
Разные фигуры имеют различное количество осей симметрии. Так у круга их бесконечное множество. У квадрата четыре оси симметрии (прямые, делящие стороны пополам, и диагонали), у прямоугольника — только две (прямые, делящие стороны пополам).
Любой правильный многоугольник имеет количество осей симметрии, равное количеству его сторон.
Осей симметрии нет у параллелограмма (кроме ромба), неравнобедренных трапеции и треугольника.
Источник: scienceland.info
Осевая симметрия


Подготовил: ученик 9 Г класса
Матвеев Илья
Учитель: Дюпина Е.А.
Симметрия относительно прямой А
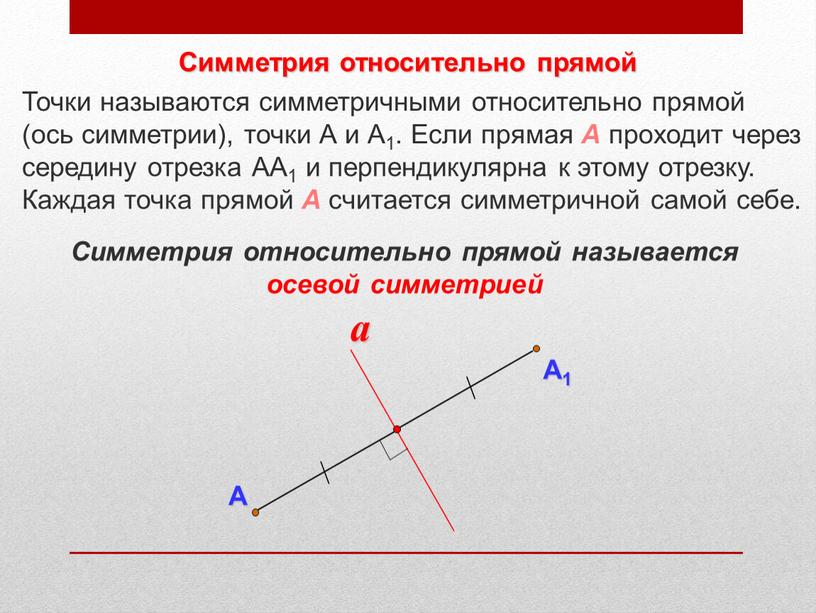
Симметрия относительно прямой
Симметрия относительно прямой называется осевой симметрией
А Построить отрезок А1В1 симметричный отрезку
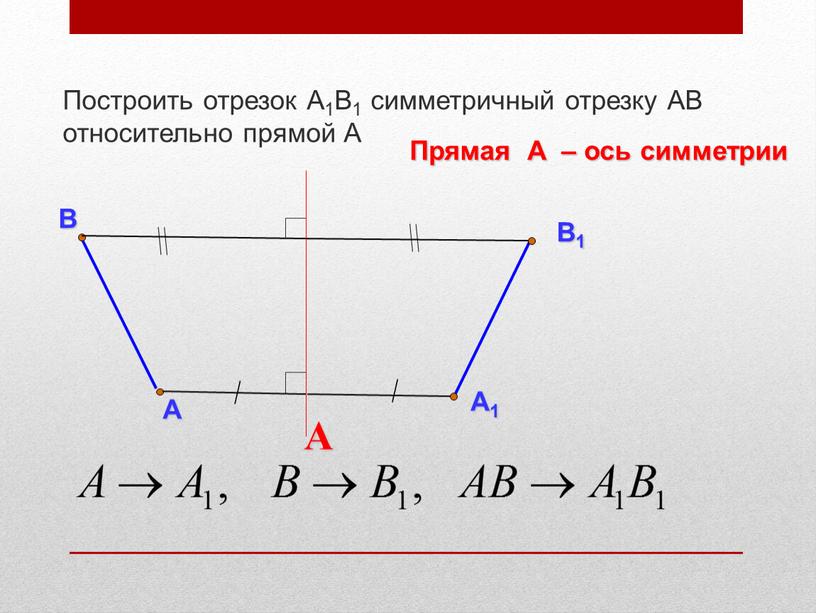
Построить отрезок А1В1 симметричный отрезку АВ относительно прямой А
Прямая А – ось симметрии
Построить отрезок А1В1 симметричный отрезку
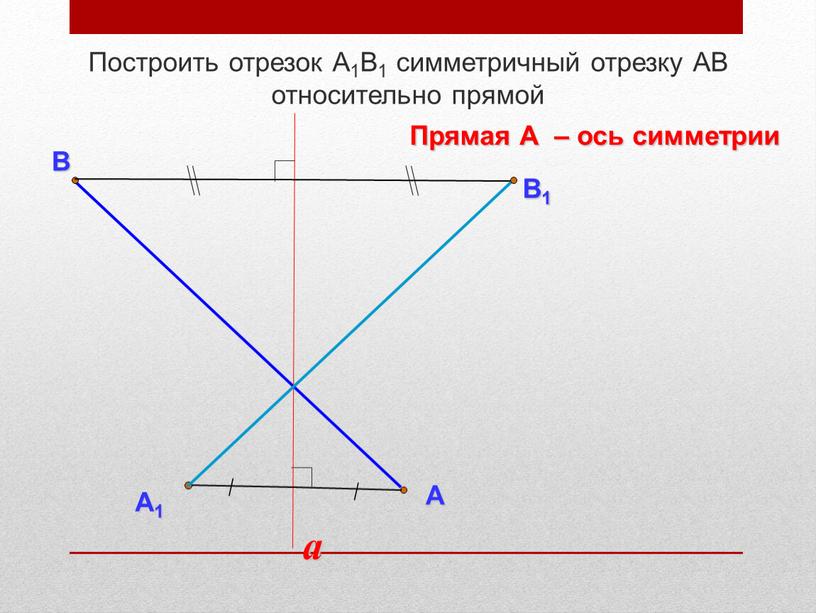
Построить отрезок А1В1 симметричный отрезку АВ относительно прямой
Прямая А – ось симметрии
Построить треугольник А1В1С1 симметричный треугольнику
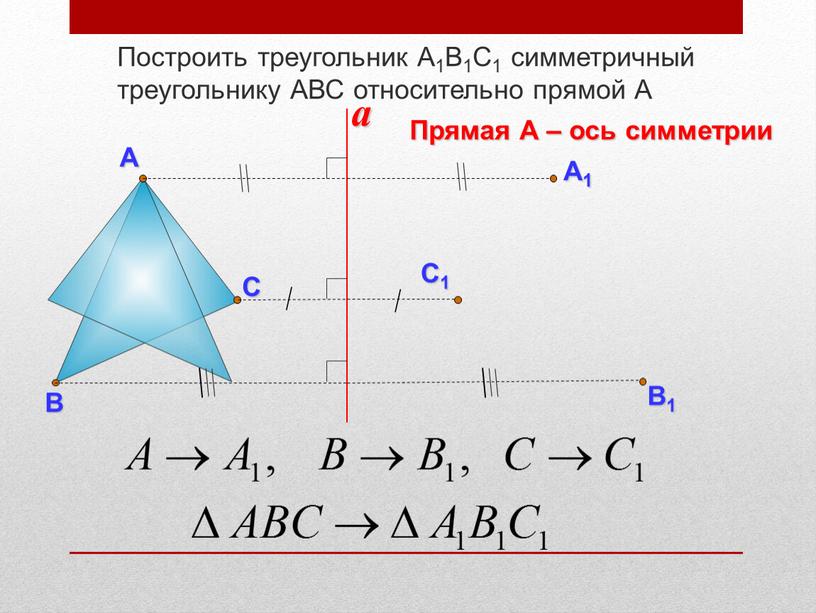
Построить треугольник А1В1С1 симметричный треугольнику АВС относительно прямой А
Прямая А – ось симметрии
Построить треугольник А1В1С1 симметричный треугольнику
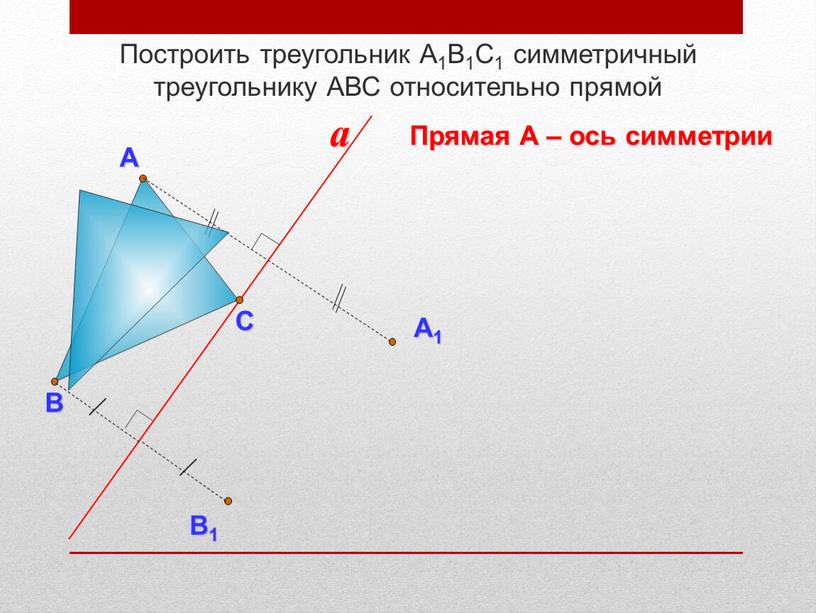
Построить треугольник А1В1С1 симметричный треугольнику АВС относительно прямой
Прямая А – ось симметрии
Построить треугольник А1В1С1 симметричный треугольнику
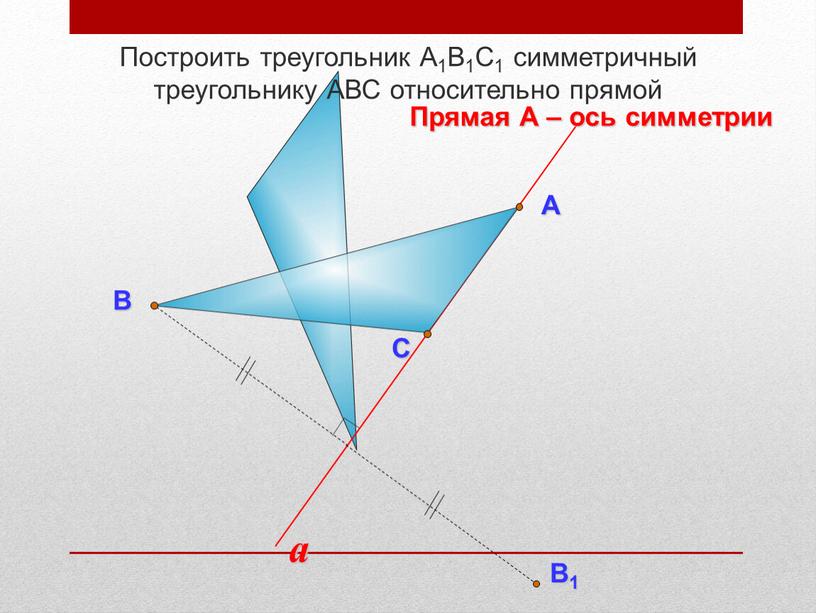
Построить треугольник А1В1С1 симметричный треугольнику АВС относительно прямой
Прямая А – ось симметрии
А В a С
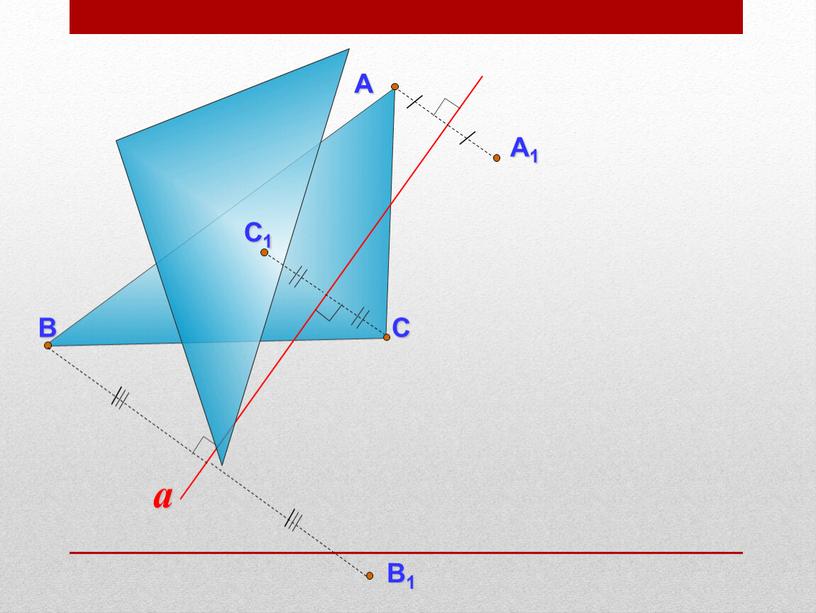
Если фигура имеет ось симметрии, то говорят, что она обладает осевой симметрией
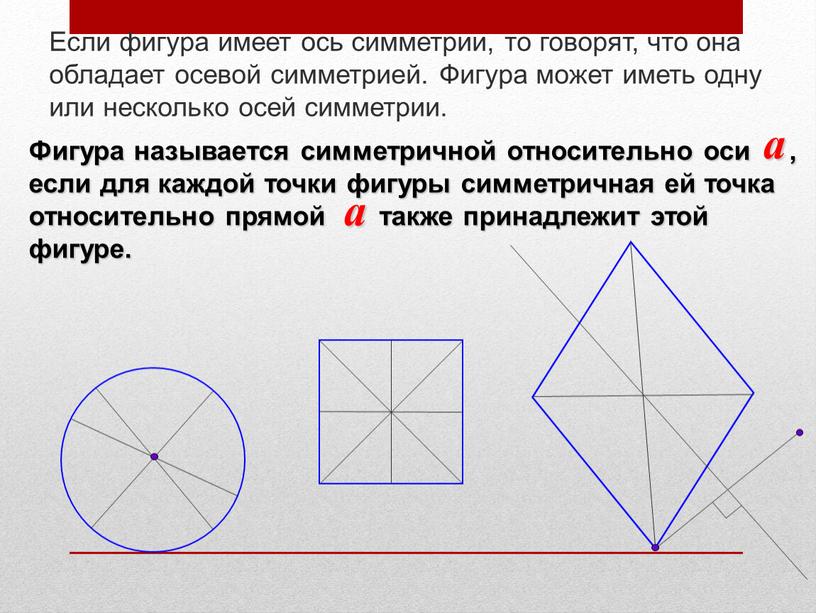
Если фигура имеет ось симметрии, то говорят, что она обладает осевой симметрией. Фигура может иметь одну или несколько осей симметрии.
Правильный треугольник Равнобедренный треугольник
Сколько осей симметрии имеет каждая фигура?
Луч Правильный шестиугольник Угол
Сколько осей симметрии имеет каждая фигура?
Какие буквы имеют ось симметрии?

Какие буквы имеют ось симметрии?
Источник: znanio.ru
