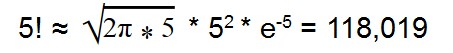В каком классе проходят факториалы по математике

Алгебра в 9 классе полна сложных и загадочных слов. Например, факториал. Давайте разберемся, что это такое и как, что и зачем с ним собственно делать.

· Обновлено 28 октября 2022

Факториал: определение

Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал».

Факториал определен для целых неотрицательных чисел. Это значит, что вот так нельзя:

• -3,75! 2,23! -2!

Число должно быть целое и положительное:

Формула факториала n!=1⋅2⋅3⋅. ⋅(n−2)⋅(n−1)⋅n

Вычисляется факториал по формуле: путем умножения всех чисел от одного до значения самого числа под факториалом. Факторизация — это разложение функции на множители.

• 3! = 1*2*3 = 6
• 4! = 1*2*3*4 = 24
• 5! = 1*2*3*4*5 = 120
• 6! = 1*2*3*4*5*6 = 720

Мы видим, что 4! — это 3!*4
5! — это 4!*5
6! — это 5!*6

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

КАК ДЕЛАТЬ ВЫЧИСЛЕНИЯ С ФАКТОРИАЛАМИ? #shorts #егэ #огэ #математика #факториал

Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.

Формулы и свойства факториала

Чтобы узнать, как вычислять факториалы быстро — воспользуемся табличкой. Сохраняйте себе и решайте раньше остальных.

Запоминаем

1! = 1

2! = 2

3! = 6

4! = 24

5! = 120

6! = 720

7! = 5040

8! = 40320

9! = 362880

10! = 3628800

11! = 39916800

12! = 479001600

13! = 6227020800

14! = 87178291200

15! = 1307674368000

16! = 20922789888000

17! = 355687428096000

18! = 6402373705728000

19! = 121645100408832000

20! = 2432902008176640000

21! = 51090942171709440000

22! = 1124000727777607680000

23! = 25852016738884976640000

24! = 620448401733239439360000

25! = 15511210043330985984000000

Факториалов в математике 9 класса — полно. Чтобы всегда быть готовым решить пример, запомните основные формулы:

• (n — 1)! = 1*2*3*4*5*. *(n — 2)(n — 1)
• n! = 1*2*3*4*5*. *(n — 2)(n — 1)n
• (n + 1)! = 1*2*3*4*5*. *(n — 2)(n — 1)n(n + 1)

С помощью формулы Стирлинга можно вычислить факториал многоразрядных чисел.

Такая формула дает результат с небольшой погрешностью.

• 

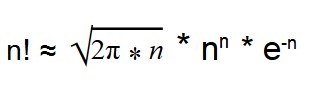Рекуррентная формула

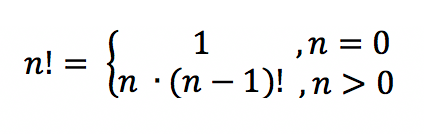• 5! = 5*(5 — 1)! = 5*4! = 5*24 = 120
• 6! = 6*(6-1)! = 6*5! = 6*120 = 720

Для решения примеров обращайтесь к таблице.

Примеры умножения факториалов:

1. Пользуйтесь готовой таблицей 5! * 7! = 120 * 5040 = 604800
2. Или раскладывайте факториалы отдельно, если хотите потренироваться:
   5! = 1*2*3*4*5 = 4! * 5 =120
   7! = 1*2*3*4*5*6*7 = 6! * 7 = 5040
   120 * 5040 = 604800

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Примеры решений

Давайте поупражняемся и решим пару примеров.

1. Сократите дробь:

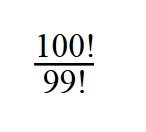
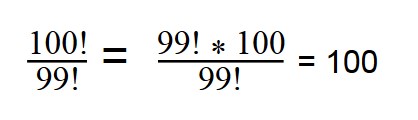
При сокращении факториалов, пользуйтесь свойством:
n! = (n — 1)! * n
100! = 99! * 100

Далее сокращаем по принципу сокращения обыкновенных дробей.

2. Вычислите значение выражения с факториалом: 8! + 5!

Можно для решения факториалов воспользоваться таблицей и вычислить быстрее.

А можно потренироваться и разложить их:

8! = 1*2*3*4*5*6*7*8 = 7!*8 = 5040 * 8 = 40320
5! = 1*2*3*4*5 = 4!*5 = 120
40320 + 120 = 40440
8! + 5! = 40440

3. Вычислите значение выражения:

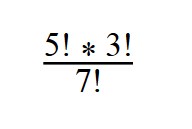
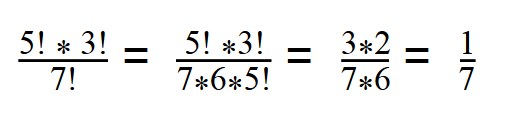
7! = 1*2*3*4*5*6*7 = 5! * 6 *7

Далее сокращаем все, что можем сократить (3*2=6, сокращаем числа 6) и получаем ответ.

4. Вычислите значение выражение:

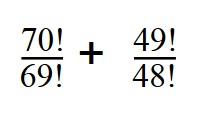
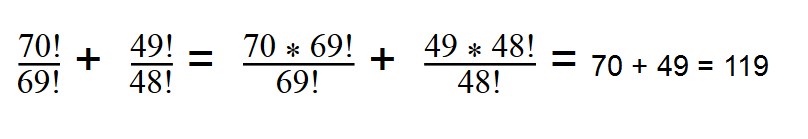
Вы уже знаете, как найти факториал — раскладываем 70 и 49:
70! = 1*2*3*. *69 = 69! * 70
49! = 1*2*3*. 49! * 48

Далее сокращаем все одинаковые множители.

5. Сократите дробь:

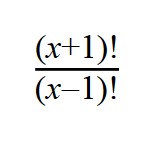
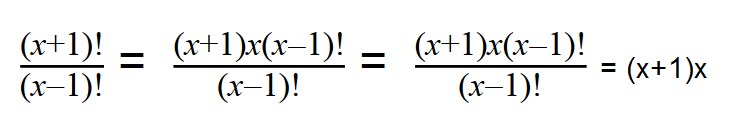
Проводим разложение на множители при помощи формул сокращенного умножения (x+1)x(x-1) и сокращаем все одинаковые множители (x-1)!.

Если вы все еще считаете, что факториал бесполезен и не может помочь вам в жизни, то это не так. Он помогает легко вычислять вероятности (а это бывает нужно чаще, чем кажется). К тому же, комбинаторика необходима тем, кто собирается работать в IT. Поэтому решайте побольше задачек на факториалы, в мире будущего без них — никуда.

Источник: skysmart.ru

Что такое факториал в математике 5 класс: Факториал — урок. Алгебра, 9 класс.

Прихожу вечером домой с работы и собираюсь традиционно у сына уроки проверять. И тут выясняется, что в домашнем задании по математике у него есть задача, которую не может решить никто. Ни он, ни мама, ни бабушка, ни дедушка… У меня глаза, понятно, загорелись – сейчас папа даст мастер-класс решения нерешаемых школьных задач и повысит свой рейтинг в глазах сына пунктов на 150.

Папа берет учебник математики за 5-й класс и читает задачу № 807: «Аня, Даша, Лена, Марина и Женя пришли к зубному врачу. Сколькими способами они могут встать в очередь?». Уп-с.

Папа помнит, что на третьем курсе универа на «Теории Вероятности» его учили решать такие задачи через факториалы. И это называется то ли «число сочетаний», то ли «число размещений» и решается как-то очень просто – факториал от пяти, что-ли…

Но папа понимает, что это задача взята из учебника для 5-го класса, где факториалов вроде как не должно быть в принципе. Значит, должно быть, какое-то другое решение – простое и понятное пятикласснику. Но все попытки найти это решение к результату не приводят. 5 девочек, 5 мест в очереди – но не 5 х 5 = 25, же, правда?

Папа начинает листать учебник, чтобы понять какую вообще дети проходят тему, что к ней такие задачи дают. Тема называется «Степени числа: квадрат, куб». Причём тут девочки в очереди и степени числа непонятно в принципе. Папа открывает ответы в конце учебника, но там нет ответа именно на эту задачу!

Папа лезет в Интернет в надежде найти какой-нибудь сайт, посвященный решениям задач по математике для пятиклассников. Зря смеетесь – папа находит и скачивает PDF-файл с ответами к задачам вроде бы этого учебника (по крайней мере, двое из четырех авторов совпадают), но выясняется, что учебник всё же другой и ответ на задачу 807 не имеет ничего общего с девочками и зубными врачами.

Папа впадает в прострацию. Но тут является счастливый сын и объявляет, что он, кажется, перепутал (!?) – им задали задачу № 801, а он написал «1» похожую на «7» (!!), вот и вышло № 807. 801-я задача, к счастью, действительно связана с квадратами и кубами, и папа с сыном легко и быстро её решают.

Но неприятный осадок, то остался! На следующее утро папа обращается к знакомым математикам и те объясняют, что это реально задача на факториалы, это действительно число сочетаний, которое считается как 5! (факториал пяти) и равно 5*4*3*2*1=120. Других вариантов решения этой задачи – для пятого класса – математики предложить не могут.

Следующим вечером папа берет в руки злополучный учебник сына по математике и, внимательно просматривая задания к теме «Степени числа», обнаруживает такие записи: «Подсчитайте: 5!, 4!, 3!». В рот мне ноги — ФАКТОРИАЛЫ! В учебнике по математике для ПЯТОГО КЛАССА! Как ты сделал это, Дэвид Блэйн? Раскукоживай обратно!

Папа осторожно спрашивает у сына, что означает вот это «5!». Сын недоуменно пожимает плечами. Папа вкрадчиво спрашивает у сына, слышал ли он раньше слово «факториал» и снова получает отрицательный ответ.

Папа остается в недоумении — то ли сын эту тему пропустил (может, пока в Таиланд ездили – хотя оттуда мы звонили и все темы, которые они проходили, разбирали), то ли она следующая в их учебном плане (факториалы? в третьей четверти пятого класса?), то ли это какой-то секретный учебник, в который вкраплены задания для вундеркиндов и фанатов теории вероятности.

Или факториалы сейчас это реально тема пятого класса? Нет, понятно, что папа учился в школе еще при Царе Горохе, но неужели умственная акселерация нового поколения зашла так далеко? Мне всегда казалось, что там в другую сторону всё движется…

И снова не могу не процитировать Пушкина: «О сколько нам открытий чудных готовит просвещенья дух…». И это только пятый класс, ребята…

Tags: семья, школа

Как объяснить факториалы? – Обзоры Вики

факториал, в математике произведение всех положительных целых чисел, меньших или равных данному положительному целому числу и обозначаемое этим целым числом и восклицательным знаком. Таким образом, факториал семь записывается как 7!, что означает 1 × 2 × 3 × 4 × 5 × 6 × 7. Факториал ноль определяется как равный 1.

Точно так же можно ли разделить факториалы? Разделение факториалов — это именно то, что он утверждает. Это задача на деление с факториалами в числителе и/или знаменателе. Например, следующее выражение представляет собой деление факториалов: 6! / 4!

Как факториалы используются в реальной жизни? Это очень полезно, когда мы пытаемся подсчитайте, сколько существует различных заказов на вещи или сколько различных способов мы можем комбинировать вещи. Например, сколькими различными способами мы можем расположить n вещей? У нас есть n вариантов для первого.

В каком классе вы изучаете факториалы? ИКЛ | факториалы | 7th класс математика

Во-вторых, можете ли вы распространять факториалы? Факторное распределение имеет место, когда набор переменных — независимые события. Другими словами, переменные вообще не взаимодействуют; Учитывая два события x и y, вероятность x не изменится, если вы умножите y. Следовательно, вероятность x при условии, что произошло y — P(x|y) — будет такой же, как P(x).

Чем полезны факториалы?

Это очень полезно, когда мы пытаемся подсчитать, сколько разных порядков существует для вещей или сколько разных способов мы можем комбинировать вещи. Например, сколькими различными способами мы можем расположить n вещей? У нас есть n вариантов для первого действия.

тогда Как вы вычисляете факториалы? Расчет факториала. Факториал n обозначается через n! и вычисляется целыми числами от 1 до n. Формула для n факториала: n! = п × (п — 1)!

Как сокращаются факториалы? Сравните факториалы в числителе и знаменателе. Расширьте больший факториал так, чтобы он включал меньшие в последовательности. Сократите общие делители между числителем и знаменателем. Упростите дальше, умножив или разделив оставшиеся выражения.

Всегда ли факториалы четны?

Факториал любого числа, кроме 1 и 0, всегда четно.

Что означает факториал в статистике? Факториал — это математическая операция, в которой вы умножаете данное число на все положительные целые числа, меньшие его. Другими словами. знак равно п × ( п — 1 ) × … × 2 × 1 .

Как вычислить вероятность с помощью факториала?

Как решить 6 факториалов?

Как вычислить факториалы на научном калькуляторе?
Может ли факториал быть нечетным?

Термин нечетный факториал иногда используется для двойной факториал нечетного номер.

Фактиарное сложение или умножение? да. Я предполагаю, что вы имеете в виду, поскольку факториал равен , аддитивный факториал будет . Число в таком виде называется треугольным числом, а формула проста.

Для чего используются факториалы в математике?

Факториал — это операция умножения любого натурального числа на все натуральные числа, которые меньше его, что дает нам математическое определение n! … Наконец, факториал используется для вопросы, которые просят вас выяснить, сколькими способами вы можете расположить или заказать определенное количество вещей.

6, 7 и 8 классы | Математика | Средняя школа | Расчеты — факториалы

Начальный (1–2 классы) Начальный (3–5 классы) Средний (6–8 классы) Младший средний (9–10 классы) Старший (11–12 классы) Испанский (все возрастные категории) ESL (все ages)GamesCup of Tea (All ages)

1. Дом
2. Средняя школа: 6, 7 и 8 классы
3. Математика: Средняя школа: 6, 7 и 8 классы
4. Вычисления — Факториалы — Введение 3 90 восклицательный знак представляет в математике?

Эта викторина по математике называется «Вычисления — Факториалы — Введение» и была написана учителями, чтобы помочь вам, если вы изучаете предмет в средней школе. Играя в образовательные викторины, вы учитесь в 6-м, 7-м или 8-м классе в возрасте от 11 до 14 лет. школьная работа. Вы можете подписаться на странице Присоединяйтесь к нам

Ах да, здесь мы столкнулись с еще одним новым словом из математического словаря — факториалов . Вы, вероятно, будете очень рады узнать, что факториалы действительно очень просты и даже забавны. Позже, когда вы продвинетесь в своих математических занятиях, таких как тригонометрия или исчисление, или даже физика, вы научитесь использовать факториалы в нескольких различных формулах. Однако для этого теста мы просто освоимся с пониманием самых основ факториалов.

Итак, что такое факториал? Факториал — это сумма всех целых чисел, умноженных в порядке возрастания, предшествующих факториальному числу, до тех пор, пока не будет достигнуто факториальное число. Что это значит? Итак, давайте посмотрим на факториал. Заводской номер 6!

Вы видели, что было выделено? 6! Восклицательный знак является частью номера. Поэтому, если вы видите цифру «6», стоящую отдельно, это просто цифра 6, но если вы видите, что она написана как « 6! », то у вас есть факториал 6!

Итак, мы узнали, что факториал — это сумма всех целых чисел, умноженных в порядке возрастания, которые предшествуют факториалу. Теперь это означает, что вы найдете все целые числа, предшествующие факториалу 6! К ним относятся числа 1, 2, 3, 4 и 5. Далее нам говорят, что мы включаем числа, пока не будет достигнуто факториальное число. Это означает, что у нас есть 1, 2, 3, 4, 5 и 6.

Далее нам говорят, что факториал представляет собой сумму целых чисел, умноженных в порядке возрастания. Это означает, что нам нужно умножать каждое число по мере восхождения к факториалу, чтобы оно выглядело следующим образом:

1 x 2 x 3 x 4 x 5 x 6

Итак, мы работаем, чтобы найти сумму.

1 х 2 = 2
2 х 3 = 6
6 х 4 = 24
24 х 5 = 120
120 x 6 = 720 (Мы остановимся здесь, поскольку мы достигли факториала. )

720 — это сумма факториала 6! Тогда эта математическая задача будет записана следующим образом.

Это также может быть записано как факториал 6! это 720 .

Видите, это действительно очень просто, не так ли? Что ж, если вы считаете, что готовы, попробуйте найти, чему равны факториалы в следующих десяти задачах.

Источник: xn—-8sbanwvcjzh9e.xn--p1ai

понятие факториала
план-конспект урока по алгебре (9 класс)

Название номинации : Урок (занятие) или методическая копилка с использованием авторских презентаций.

Тема урока : Перестановки. Факториал.

Тема «Факториал» занимает важное место в разделе « Комбинаторики»

На данном уроке вводится понятие факториала, решение простых задач на перестановки, преобразование и нахождение значений выражений, содержащих факториалы. Приложения содержат достаточно материала для отработки данных навыков. Презентация позволяет эффективно провести устный счёт, на каждом этапе урока делать проверку, познакомить с историческими данными. Урок может быть полезен учителям математики.

Многие годы « элементы статистики, комбинаторики и теории вероятностей» не изучалась в школе. Проработав в школе много лет, учителям приходится заново самим изучать данные темы и продумывать методику их преподавания. Именно тема « Факториал» является базовой для решения задач на размещения, перестановки и сочетания и от того как учащиеся усвоят данную тему зависит на сколько успешны они будут при решении более сложных комбинаторных задач.

1. Обратить внимание на значимость темы « Факториал».
2. Разработать методику преподавания данной темы.
3. Подобрать дидактический материал.

На уроке используются различные формы самостоятельной работы:

1. Работа с учебником.
2. Работа в группе.
3. Работа в паре.
4. Самостоятельная работа на 2 варианта.

После каждого этапа работы проводится проверка, выполненных заданий. Проведение и проверка самостоятельной работы в конце урока дают возможность оценить степень усвоения данной теме, что позволяет целенаправленно планировать следующие уроки. Презентация на разных этапах урока решает задачи:

1. Эффективно провести устный счёт.
2. Делать проверку, выполненных заданий.
3. Познакомить с историческими данными.
4. Подвести итоги урока.

Данный урок рассчитан на учебник А.Г. Мордкович. Алгебра. 9класс. В 2 ч. – М.;Мнемозина,2010., поменяв домашнее задание, урок может быть использован применительно к любому другому учебнику.

ТЕМА УРОКА «Перестановки. Факториал»

Образовательная цель : дать специальное название одному из видов комбинаций – перестановки, рассмотреть формулу для вычисления числа перестановок, ввести понятие факториала, решение простых задач на перестановки, преобразование и нахождение значений выражений

Развивающая цель : способствовать формированию логического мышления учащихся при решении задач и развитию монологической речи обучающихся с использованием новых терминов.

Воспитательная цель : приучать школьников к доброжелательному общению в группе, в паре. развитие умений оценивать результаты своей работы на уроке, регулировать и контролировать свои действия .

1. Организационный момент. (2мин)
2. Устная работа. (5мин)
3. Новая тема.(7мин)
4. Работа в группах (7+1мин)
5. Работа в парах (7+1 мин)
6. Самостоятельная работа. (6+1мин)
7. Подведение итогов (3мин).

В течении урока учащиеся заполняют оценочную таблицу и в конце урока выставляют себе оценки.

Оценки: 14-17баллов-3, 18-22баллов -4, 23-29баллов -5.

1. Учитель знакомит учащихся с темой и целями урока.( слайд1-2)
2. Устная работа На прошлом уроке мы начали решать комбинаторные задачи. Каким правилом мы пользовались? (слайд3-6)

А) сколько четных трёхзначных чисел можно составить из цифр 2.3,4,5,

Б) В столовой имеются 3 первых блюда, пять вторых блюд и 2 третьих. Сколькими способами посетитель может выбрать обед, состоящий из 3-х блюд.

В)Проказница Мартышка
Осел,
Козел,
Да косолапый Мишка
Затеяли играть квартет
…
Стой, братцы стой! –
Кричит Мартышка, — погодите!
Как музыке идти?
Ведь вы не так сидите…
И так, и этак пересаживались – опять музыка на лад не идет.
Тут пуще прежнего пошли у них раздоры
И споры,
Кому и как сидеть…

Вероятно, крыловские музыканты так и не перепробовали всех возможных мест. Однако способов не так уж и много. Сколько?

Попробуем решить эту задачу. К доске вызываются 4 ученика. На доске

Появляется запись. 4*3*2*1.=24.

1. Мы получили произведение первых четырёх натуральных чисел. Оказывается произведение подряд идущих первых натуральных чисел часто встречается при решении комбинаторных задач, поэтому для обозначения таких произведений ввели новое понятие факториал.

Работа по учебнику. Стр.180. определение факториала. Свойство факториала, формула. (слайд7)

Термин «факториал» ввёл Л. Арбогаст (1800), обозначение n ! – К. Крамп (1808)

Рассмотрение примеров.(слайд 9)

а) 4! = 1*2*3*4 = 24;
б) 5! = 1*2*3*4*5* = 120; учитель обращает внимание на таблицу.
в) 4! + 5! = 1*2*3*4 + 1*2*3*4*5 = 24+120 = 144;
г) 5*4! =5* 1*2*3*4 = 5! = 120;
(письменно): д) 4! * 5! = 1*2*3*4 *1*2*3*4*5 = 24 * 120 = 2880;

Учитель. Принято считать: 1!=1, 0!=1. (слайд10)

Факториалы растут удивительно быстро. Вы можете понаблюдать за их изменением, рассмотрев таблицу в учебнике, в которой приведены факториалы чисел от 1 до 10:

А значение выражения 15!, которого нет в таблице, превосходит 10 15 , а именно 15!=1 307 674 368 000. Может быть, именно из-за быстрого роста факториалов восхищенный изобретатель этого выражения использовал восклицательный знак.

Вернёмся к первой задаче.

Число всевозможных перестановок из n элементов обозначают

P n (P – первая буква французского слова permutation – перестановка). Читается: “Число перестановок из эн элементов” или “Пэ из эн”.

В задании 1 было показано P 4 = 4*3*2*1 = 1*2*3*4 (по переместительному свойству умножения).

т.о., число перестановок из n элементов равно произведению всех натуральных чисел от 1 до n.

При использовании символа n! формула (1) принимает вид P n = n! (слайд11)

Обращать внимание учащихся при решении задач на следующие факты :

1) в задачах на перестановки используются все элементы данного набора элементов;

2) две перестановки одного набора элементов отличаются друг от друга только порядком элементов)

4. Работа в группах.(слайд12 )

1задание . Разобрать решение предложенных задач.

1. Пример 1. В расписании 7 класса на четверг должно быть 6 предметов: русский язык, литература, алгебра, география, физика, физкультура. Сколькими способами можно составить расписание на этот день?
2. Решение. Число способов, которыми можно составить расписание, равно числу перестановок из шести элементов: P 6 =6!=1*2*3*4*5*6=720.
3. Пример 2. Сколькими способами можно составить расписание из тех же 6 предметов, если требуется, чтобы урок физкультуры был последним?
4. Решение. У урока физкультуры фиксированное место, поэтому расписания отличаются порядком остальных 5 предметов. Значит, число таких расписаний равно числу перестановок из 5 элементов: P 5 =5!= 120.
5. Пример 3. Сколькими способами из тех же 6 предметов можно составить такое расписание, в котором русский язык и литература стоят рядом?
6. Решение. Будем рассматривать русский язык и литературу как один предмет, тогда всего предметов будет пять. Число способов, которыми можно составить расписание из 5 предметов, равно P 5 =5!. Но в каждой из этих перестановок русский язык и литература могут меняться местами. Поэтому искомое число расписаний вдвое больше. Оно равно 5!*2=240.

1. Сколькими способами можно выписать в колонку фамилии 30 учеников?

Решение . P 30 = 30!

2. Сколько различных 5-значных чисел, все цифры которых различны можно записать с помощью цифр 4, 5, 6, 7, 8?

Решение . Задача сводится к подсчету числа перестановок из 5 элементов. P 5 = 1*2*3*4*5 = 120. Ответ : 120 различных чисел.

3. Сколькими способами можно расставить на полке 8 книг, если среди них 2 книги одного автора, которые при любых перестановках должны стоять рядом?

Решение: первоначально будем считать 2 книги одного автора единой книгой. Тогда количество способов расстановки условных семи книг на полке будет равно числу перестановок из 7 элементов: P 7 = 1*2*3*4*5*6*7 = 5040. Но в каждой такой перестановке книги одного автора можно менять местами, потому общее число способов расстановки книг на полке будет в 2 раза больше, т.е. 5040 * 2 = 10080.

Ответ : 10080 способов.(стр. 47 МШ — 3 — 2003).

; 5 .Работа в парах. (слайд14)

1. Сколькими способами можно рассадить 15 учеников на ЕГЭ по математике за 15-ю партами
2. а) ; б) ;
3. Упростить:

Источник: nsportal.ru