В каком классе проходят степени по математике

Содержание

Степень числа – это многократное повторение умножения числа на само себя.

Степень числа записывается в виде числового знака, расположенного над числом. Знак имеет меньший размер, чем само число и обозначает количество раз, которое число умножается на само себя. Число операций умножения называется показателем степени числа, а само число выступает основанием степени.

Степень числа изучается в курсе алгебры средней общеобразовательной школы, начиная с седьмого класса.

Принципы изучения степени числа в общеобразовательной школе

Изучение степени числа в курсе алгебры начинается с седьмого класса. Обучение начинается с познания степени с натуральным показателем. Полноценно изучив данную тему, происходит переход к познанию степени отрицательного числа, а затем изучается степень с целым показателем и степень с рациональным показателем. Во время изучения, осуществляется освоение выполнения различных операций с числами и их степенями.

Профориентация для студентов

Поможем определиться с профессией, окажем помощь в профессиональном самоопределении и трудоустройстве

Возведение числа в степень n первоначально основывалось на понимании повторения данного числа некоторое количество раз, а именно n –ое количество. При этом, не рассматривалось операций с отрицательными основании и отрицательными степенями, а также степенями с рациональными показателями. Только в конце XVII Ньютоном было дано определение степени числа, его значение, рассмотрены числа с различными степенями и операции с ними.

Изучение степени числа реализуется на основании соблюдения ряда принципов:

Принцип доступности. В данном случае, огромную роль играет доступность изложения материала. Педагог должен начинать с простых понятий и переходить постепенно к более сложным. Кроме того, необходимо опираться на аналогии и сравнения в объяснении, давать наглядные примеры и демонстрировать практическое использование теории в решении арифметических задач на нахождение степени числа и совершения иных операций со степенями. Как правило, педагог составляет алгоритм решения задач и добивается запоминания учащимися последовательности совершения арифметических действий.
Принцип наглядности. Обучение арифметическим операциям со степенями должно быть реализовано с помощью наглядных примеров действий. Актуально применение графиков и диаграмм, демонстрирующих натуральные числа и их переходы в степень с помощью линий и отрезков или движения изображения переменной величины. Хорошо выстраивать таблицы с числовыми значениями и отображать их переходы в различные степени с помощью графика. Это не только делает объяснение более понятным для учащихся, но и развивает их интерес к совершению математических операций с различными степенями чисел.
Принцип активности. Предполагается, что учащиеся должны проявлять активность в познании степени числа и стремиться совершать различные арифметические действия с числами и степенями. Для этого, используются приемы интересной подачи нового материала.
Принцип концентричности. Изучение степени числа реализуется в средней и старшей школе. Например, в пятом классе учащиеся узнают, что представляет собой квадрат числа и как он записывается. При этом, они не изучают никаких операций с квадратом числа. Первоначальное представление о степени числа формируется в курсе алгебры в 7-ом классе. Происходит освоение понятия степени числа, изучаются свойства и осваиваются простые операции со степенями. Далее, знания расширяются и углубляются.

«Формирование понятия степень числа в курсе алгебры основной школы»
Готовые курсовые работы и рефераты
Консультации эксперта по предмету
Помощь в написании учебной работы

Методика изучения степени числа с натуральным показателем

Изучение степени числа с натуральным показателем реализуется поэтапно:

Знакомство с понятием степени числа с натуральным показателем. Учащимся объясняется, что степенью числа а, с натуральным показателем n, который больше одного, называется произведение показателя n на число а. Запись данной операции имеет следующий вид: $a^ⁿ = a • a • a • a….$ n-е количество раз.
Освоение понятия «возведение в степень» и нахождение степени числа. Здесь, учащимся дается информация о том, что если в степень возводится положительное число, то и ответ будет положительным числом, а если отрицательное, то получается отрицательное число или положительное: все зависит от степени числа (если степень имеет четное число, то результат будет положительным, а если нечетное, то отрицательным. Если возвести в степень нуль, то и ответ будет равен нулю.
Освоение операций на умножение степеней с одинаковым основанием. Изучается основное правило умножение степеней: сохранение значения основания числа и сложение его степеней т.е. $а^ⁿ • а^ⁿ = а^$.
Освоение выполнения операций по возведению степени числа в степень. Осваивается правило возведения степени числа в степень: сохранение основания и умножение степеней друг на друга т.е. $(а^ⁿ)^ ⁿ= а^$
Освоение возведения степени произведения чисел. Осваивается правило совершения данной операции: возведение в степень каждого основания и их умножение друг на друга т.е. $ab^ⁿ = а^ⁿ • b^ ⁿ$.
Освоение возведения в степень дроби. Осваивается правило совершения данной операции: поочередное возведение в степень числителя и знаменателя т.е. $(а/b)^ ⁿ= а^ ⁿ/b^ ⁿ$.

Изучение степени отрицательного числа и степени с рациональным показателем

Методика изучения данных степеней реализуется в следующей последовательности:

Рассмотрение степени отрицательного числа с четным и нечетным показателем: их понятие и различия или изучение понятия степени с рациональным показателем. Степень отрицательного числа с четным показателем является положительным числом, а степень отрицательного числа с нечетным показателем является отрицательным числом. Это объясняется правилами умножения: умножение четных отрицательных чисел дает положительный результат, а нечетных отрицательных множителей – отрицательный. Степень с рациональным показателем представляет собой число с основанием а, степенью которого является дробь т.е. $а^< ⁿ/ m>$.
Изучение особенностей совершения различных арифметических действий с отрицательными числами и степенями с рациональным показателем. Осваиваются основы их умножения, деления, возведения в степень.
Закрепление теоретической информации выполнением практических арифметических примеров на данные темы.

Источник: spravochnick.ru

Свойства степеней. Действия со степенями

В этой статье разберем основные свойства степеней, а также какие операции со степенями возможны в математике. А еще изучим свойства степеней с разными и одинаковыми основаниями и, конечно, потренируемся на примерах.

29 сентября 2020

· Обновлено 28 октября 2022

Что такое степень числа

В учебниках по математике можно встретить такое определение:

«Степенью n числа а является произведение множителей величиной а n раз подряд»

a — основание степени;

n — показатель степени.

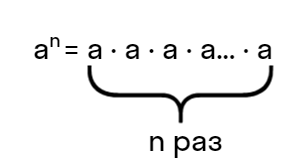
a в степени n

Читается такое выражение, как a в степени n

Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) само на себя.

А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:

2 3 = 2·2·2, где:

2 — основание степени;

3 — показатель степени.

Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.

Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.

Задачка про миллион: представьте, что у вас есть миллион рублей. За один год вы заработали на нем еще два. Еще через год каждый миллион принес еще два и т. д. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда?

А теперь посчитаем, какая сумма у вас будет через 4 года.

Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:

3·3·3·3 = 81. То есть получается, что три в степени четыре равно 81.

Математики заскучали и решили все упростить:

Ответ: через четыре года у вас будет 81 миллион.

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

Источник: skysmart.ru

Степень — свойства степеней — видеоурок

Видео урок по алгебре для 7 класса. На этом видео уроке объяснятся: — что такое степень с натуральным показателем — что такое натуральные числа — как умножить степени и одинаковыми основаниями — как разделить степени и одинаковыми основаниями — как возвести степень в степень решается номер 377, 409 и 415 из учебника Макарычева по алгебре 7 класса на степени с натуральными показателями и свойства степеней.